Illustrative examples
In this chapter, we demonstrate the use of Xpress-SP's modeling and solution techniques in solving stochastic problems from various streams such as supply chain management, finance, energy sector, transportation, and forest planning. A short description of a problem from each sector is given, followed by the model used to solve the problem and its implementation with Mosel.
Farm production planning
In this section, we show how to model a simple 2-stage model using Xpress-SP. We model the farmer's problem (see [BL97a]), where a farmer needs to make decisions regarding the devotion of available land to different products: wheat, corn and sugar beet, during the winter season. The yield is realized in the summer and depends on the overall weather during the year (e.g., bad, ok, good). The farmer must produce a certain amount of products for the cattle feed. Then the farmer must also decide how much of each product needs to be purchased or sold depending on the yield. There is an additional restriction on the selling price of sugar beet because of quota restriction. The model entities are described below.
- Sets
- Stages: {Winter, Summer}
- Products: {Wheat, Corn, Sugar Beet}
- Constraints
- Minimum production for cattle feed
- Quota restriction on sugar beet production
- Variables
- xi: acres of land devoted to product i
- wwheat, wcorn: tons of wheat and corn sold respectively
- ywheat, ycorn: tons of wheat and corn purchased respectively
- wfavor, wunfavor: tons of sugar beet sold at favorable and unfavorable price respectively
Model
model farmer
uses 'mmsp'
parameters
Explicit=false ! Explicitly create tree or use the joint
! distribution feature
end-parameters
forward procedure Analyse(prob: string)
setparam('xsp_scen_based', false)
declarations
!{"Wheat","Corn","Sugar Beet Favorable","Sugar Beet Unfavorable"}
AllProducts={"Wht","Crn","SugBtFav","SugBtUnfav"}
Products={"Wht","Crn","SugBt"}
WheatAndCorn={"Wht","Crn"}
PlantingCost: array(Products) of real
SellingPrice: array(AllProducts) of real
PurchasePrice: array(WheatAndCorn) of real
MinimumRequirement: array(WheatAndCorn) of real
TotalAvailableLand: real
MaxSugarBeetQuota: real
end-declarations
PlantingCost:= [150,230,260]
SellingPrice:= [170,150,36,10]
PurchasePrice:= [238,210]
MinimumRequirement:= [200,240]
TotalAvailableLand:= 500
MaxSugarBeetQuota:= 6000
declarations
Stages={"Wint","Summ"}
yield: array(Products) of sprand
x: array(Products) of spvar
y: array(WheatAndCorn) of spvar
w: array(AllProducts) of spvar
TotalCost: splinctr
LandUtilized: splinctr
MinCattleFeedRequirement: array(WheatAndCorn) of splinctr
SugarBeetProduction: splinctr
SugarBeetQuota: splinctr
end-declarations
! Stages
spsetstages(Stages)
forall(p in Products) spsetstage(yield(p),"Summ")
! Scenarios
declarations
S = 3
Values: array(Products,1..S) of real
end-declarations
forall(s in 1..S) prob(s):=1/3
Values:= [3,2.5,2,
3.6,3,2.4,
24,20,16]
if Explicit then
spcreatetree(S)
spsetprobcond(2,prob)
forall(p in Products,s in 1..S)
spsetrandatnode(yield(p),s,Values(p,s))
spgentree
else
spsetdist(union(p in Products) {yield(p)},Values,prob)
spgenexhtree
end-if
! Model
TotalCost:= sum(p in Products) PlantingCost(p)*x(p)-
sum(p in AllProducts) SellingPrice(p)*w(p)+
sum(p in WheatAndCorn)PurchasePrice(p)*y(p)
LandUtilized:= sum(p in Products) x(p) <= TotalAvailableLand
forall(p in WheatAndCorn)
MinCattleFeedRequirement(p):= yield(p)*x(p)+y(p)-
w(p) >= MinimumRequirement(p)
SugarBeetProduction:= sum(p in {"SugBtFav","SugBtUnfav"})
w(p)<=yield("SugBt")*x("SugBt")
SugarBeetQuota:= w("SugBtFav") <= MaxSugarBeetQuota
forall(p in Products) spsetstage(x(p),"Wint")
forall(p in WheatAndCorn) spsetstage(y(p),"Summ")
forall(p in AllProducts) spsetstage(w(p),"Summ")
! Analysis
declarations
Problem={"Rec","Exp Val","Exp Val wt rec","Perf Inf",
"Perf Inf wt rec"}
end-declarations
forall(problem in Problem) Analyse(problem)
!***************************************************************
procedure Analyse(problem:string)
write("Solving " + problem + " Problem")
case problem of
"Exp Val": minimize(TotalCost,XSP_EV)
"Exp Val wt rec": minimize(TotalCost,XSP_EV+XSP_REC)
"Perf Inf": minimize(TotalCost,XSP_PI)
"Perf Inf wt rec": minimize(TotalCost,XSP_PI+XSP_REC)
"Rec": minimize(TotalCost,XSP_REC)
end-case
writeln("\n------------------------------------------")
write("Culture |")
forall(p in Products) write(strfmt(p,7))
writeln("\n------------------------------------------")
if(problem="Perf Inf") then
forall(s in 1..spgetscencount) do
write("Surface (acres) ",s," |");
forall(p in Products) write(strfmt(getsolinscen(x(p),s),7,2));
writeln
end-do
else
write("Surface (acres) |");
forall(p in Products) write(strfmt(speval(x(p)),7,2))
writeln
end-if
writeln("TotalProfit=$",-getobjval)
writeln("------------------------------------------")
case problem of
"Exp Val wt rec","Perf Inf wt rec":
do
forall(p in Products) spunfix(x(p))
spsethidden(LandUtilized,false)
end-do
end-case
writeln
end-procedure
end-model
Results
The overall expected profit is $108,390. The solution, which was obtained considering all circumstances, is ideal. It also allows selling some sugar beet at an unfavorable price or having unused quota and hence hedging against various scenarios. The model also provides the option of either creating the scenario tree explicitly or using the joint distribution functionality in mmsp. The following output is obtained after the model is run in Xpress-SP.
Solving Rec Problem
------------------------------------------
Culture | Wht Crn SugBt
------------------------------------------
Surface
(acres) | 170.00 80.00 250.00
TotalProfit=$108390
------------------------------------------
Solving Exp Val Problem
------------------------------------------
Culture | Wht Crn SugBt
------------------------------------------
Surface
(acres) | 120.00 80.00 300.00
TotalProfit=$118600
------------------------------------------
mmsp warning 101: fixing variables and hiding constraints
mmsp warning 102: hiding constraint, since all variables are hidden/fixed
Solving Exp Val wt rec Problem
------------------------------------------
Culture | Wht Crn SugBt
------------------------------------------
Surface
(acres) | 120.00 80.00 300.00
TotalProfit=$107240
------------------------------------------
Solving
Perf Inf Problem
------------------------------------------
Culture | Wht Crn SugBt
------------------------------------------
Surface
(acres) 1 | 183.33 66.67 250.00
Surface
(acres) 2 | 120.00 80.00 300.00
Surface
(acres) 3 | 100.00 25.00 375.00
TotalProfit=$115406
------------------------------------------
mmsp warning 101: fixing variables and hiding constraints
mmsp warning 102: hiding constraint, since all variables are hidden/fixed
Solving
Perf Inf wt rec Problem
------------------------------------------
Culture | Wht Crn SugBt
------------------------------------------
Surface
(acres) | 134.44 57.22 308.33
TotalProfit=$103717
------------------------------------------
Finance
Stochastic programming has been extensively studied and applied in various sectors of finance, e.g., asset liability management, portfolio management, financial planning, etc. Here we consider a simple stochastic problem for financial planning [BL97b].
Model description
We currently want to invest $b in stocks and bonds. At the end of T-1 years, we would like to exceed the goal $G. The investment is changed every year. The excess income would imply an income of q% of the excess income and shortage would imply borrowing at r% of the amount short. The plot of the utility function for wealth at the end would look as follows:
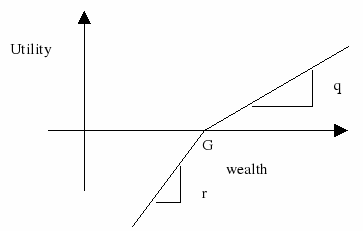
Figure 6.1: Utility function
We also assume that at each stage the return on stocks and bonds is 1.25 and 1.14 or 1.06 and 1.12 each with probability 0.5
- Decision variables
- xit: amount invested in asset i at time t
- y: shortage
- w: excess
- Constraints
- Balance of initial investment, returns and goal meeting requirements
Xpress model
model stochasticStockAndBondModel
uses 'mmsp'
parameters
T=4
Explicit=true
end-parameters
forward procedure generateTree
declarations
Assets={"Stocks","Bonds"}
Stages=1..T
x: array(Assets,1..T-1) of spvar ! Amount invested
w,y: spvar ! Shortage, excess
return: array(Assets,2..T) of sprand ! Return on investment
b,G: real ! Initial wealth, goal(in $1000)
q,r: ! Excess,shortage(in %)
ExpectedUtility: splinctr
Balance: array(1..T) of splinctr
end-declarations
! Data
b:=55;G:=80;q:=1;r:=4
spsetstages(Stages)
forall(i in Assets,t in 2..T) spsetstage(return(i,t),t)
generateTree
forall(i in Assets,t in 1..T-1) spsetstage(x(i,t),t)
spsetstage(y,T)
spsetstage(w,T)
ExpectedUtility:=q*y-r*w
forall(t in 1..T)
if t=1 then
Balance(t):=sum(i in Assets) x(i,t)=b;
elif t=T then
Balance(t):=sum(i in Assets) return(i,t)*x(i,t-1)- y+w=G;
else Balance(t):=-sum(i in Assets) x(i,t)+
sum(i in Assets) return(i,t)*x(i,t-1)=0;
end-if
setparam("xsp_scen_based",false)
setparam('xsp_verbose',false)
maximize(ExpectedUtility)
ObjvalRP:=getobjval
writeln("Obj value in recourse problem = ", strfmt(ObjvalRP,0,2))
forall(t in 1..T-1) spfix(x("Bonds",t),0)
maximize(ExpectedUtility)
writeln("Obj value in recourse problem = ", strfmt(getobjval,0,2))
writeln("VSS (if all investments in Stocks only) = ", strfmt(ObjvalRP-
getobjval,0,2))
forall(t in 1..T-1) spunfix(x("Stocks",t))
!***********************************************************
procedure generateTree
declarations
SetSrnd: set of sprand
val: array(1..2,1..2) of real
prob: array(1..2) of real
StockVal,BondVal,BranchProb: array(1..2) of real
end-declarations
if(Explicit) then
spcreatetree(2) ! Binary tree
StockVal:=[1.25,1.06]
BondVal:=[1.14,1.12]
BranchProb:=[.5,.5]
forall(t in 2..T) do ! Set Srnds
spsetrand(return("Stocks",t),StockVal)
spsetrand(return("Bonds",t),BondVal)
end-do
spsetprobcond(BranchProb) ! Set branch probabilities
spgentree ! Generate tree
else ! Use joint distribution functionality
val:=[1.25, 1.06, 1.14, 1.12]
prob:=[.5, .5]
forall(t in 2..T) do
SetSrnd:={}
forall(i in Assets) SetSrnd+={return(i,t)}
spsetdist(SetSrnd,val,prob)
end-do
spgenexhtree
end-if
end-procedure
end-model
Note that in the above model, users may implicitly set the stages of return and x by setting the control parameter xsp_implicit_stage to true, but this would also set the variables w and y to the first stage, therefore their stages have to be set explicitly using the function spsetsatage().
Results
The optimal value of expected utility is –1.514. The initial investment in stocks and bonds is $41479 and $13520 respectively. The model also demonstrates how users may fix certain decisions and solve the problem in the stochastic framework. In the above model, the impact of placing all the funds in stocks is evaluated. It is observed that the expected utility using this strategy is -3.79. Other results can be analyzed in IVE.
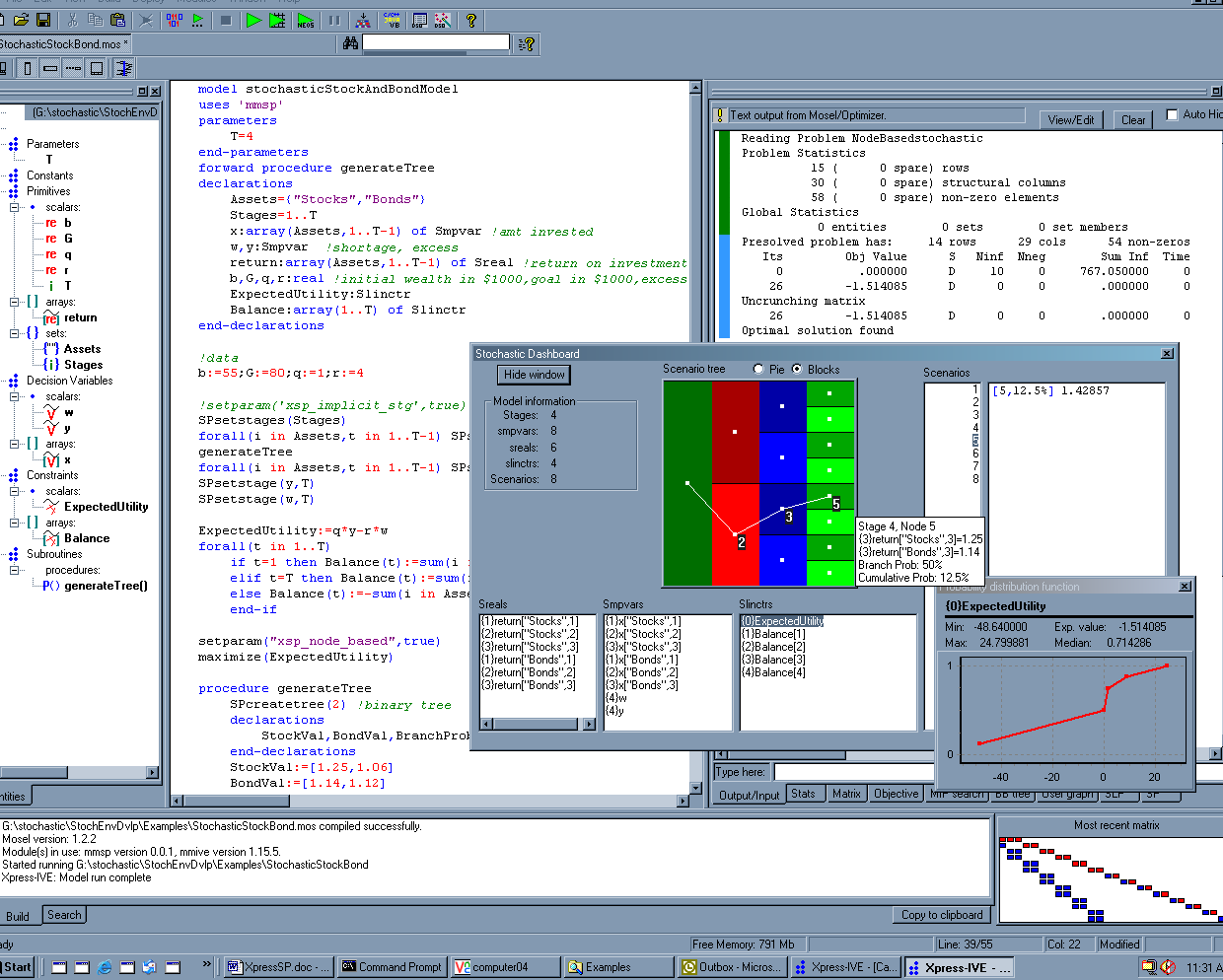
Figure 6.2: Stocks and bond model in IVE
Energy
Stochastic programming also finds wide-spread application in the energy sector where the demand for power and its prices are constantly changing. It has been used for solving various problems such as capacity expansion, unit commitment, etc. Here, we discuss an implementation of a capacity expansion model using Xpress-SP.
Model description
In a power-generating plant, the trend of yearly power demand looks as follows:
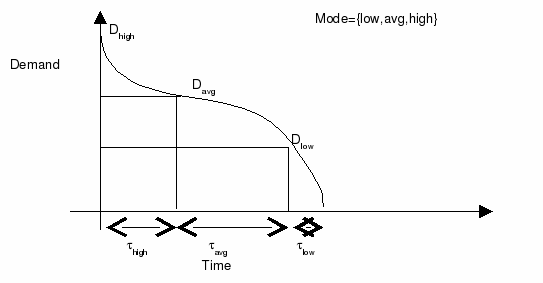
Figure 6.3: Load duration curve
Here, for simplicity, we consider three modes of operations; namely low, average, and high. Clearly, the trend of power demanded in each year may vary depending on various factors such as rainfall, weather conditions, etc. We also consider three technologies (old, current, and new). Capacity expansion plans and the operational decisions need to be laid out for next three years. The objective is to minimize the expected total investment and production cost. The stochastic model entities are described below.
- Parameters
- Stages = 1,...,4 : indexed by t
- Technology = {old,curr,new} :indexed by i
- Modes={low,avg,high} :indexed by j
- Data
- git: existing capacity of technology i added at time t
- rit:investment cost per unit of capacity of technology i added at time t
- qit:production cost per unit of capacity of technology i added at time t
- Decision variables
- xit: capacity of technology i added at time t
- yijt:capacity of type i dedicated in mode j at time t
- Constraints
- Accumulated Capacity balance
- Demand balance
- Objective
- minimize the expected total investment and production cost
The capacities are added in the first two years and hence the total available capacities are realized in the second and the third year. In the years two through four, the available capacities are distributed among different modes.
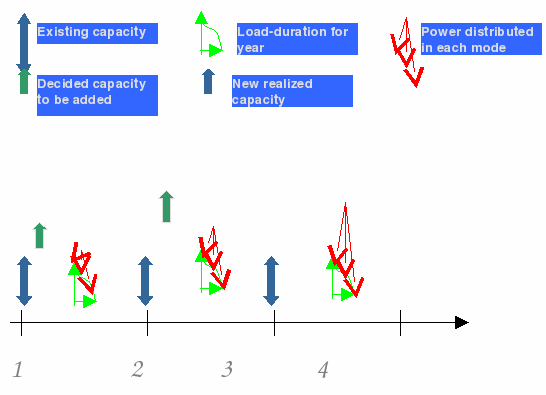
Figure 6.4: Production planning schedule
The scenarios are created by discretizing the load-duration curve. For simplicity, the duration in each mode is considered one-third of a year. We present three ways of generating scenarios:
- Exhaustive: The demand (low, average, and high) has an independent distribution in each year.
- Stage symmetric: There are 8, 5, and 3 load-duration curves possible in the first, second, and third year respectively.
- Explicit: The demand in the subsequent year depends on the earlier years' demand and hence, all possible realizations are explicitly defined.
Exhaustive model
model CapacityExpansion
uses 'mmsp'
parameters
T=4 ! Years
end-parameters
forward procedure generateExhaustiveTree
declarations
Stages=1..T
Technology={"old","curr","new"}
Modes={"low","avg","high"}
r: array(Technology,1..T-2) of real ! Investment cost in $1000/MW cap. added
g: array(Technology,1..T-1) of real ! Existing capacity in MW
q: array(Technology,2..T) of real ! Unit production cost in $1000/MWh
tau: real ! Time in hour spent in each mode
Budget: real ! Max. additional capacity in MW
Penalty: real ! For not meeting demand in $1000/MW
d: array(Modes,2..T) of sprand ! Total demand in MW
umd: array(Modes,1..T-1) of spvar ! Total unmet demand in MW
x: array(Technology,1..T-2) of spvar ! Additional capacity in MW
w: array(Technology,2..T-1) of spvar ! Total available capacity in MW
y: array(Technology,Modes,2..T) of spvar ! Capacity used in production in MW
Cost: splinctr
BudgetSpent: splinctr
AccumulatedCapacity: array(Technology,2..T-1) of splinctr
Demand: array(Modes,1..T-1) of splinctr
Capacity: dynamic array(Technology,1..T-1) of splinctr
end-declarations
! Read in data from external file
initializations from 'CapacityExpansion.dat'
r q g tau Budget Penalty
end-initializations
setparam('xsp_implicit_stage',true)
spsetstages(Stages)
generateExhaustiveTree
Cost:= sum(t in 1..T-2,i in Technology) r(i,t)*x(i,t) +
sum(t in 2..T,i in Technology,j in Modes) q(i,t)*tau*y(i,j,t) +
sum(j in Modes,t in 1..T-1) Penalty*umd(j,t)
BudgetSpent:= sum(i in Technology,t in 1..T-2) x(i,t)<=Budget
forall(i in Technology,t in 2..T-1)
if (t-1>=2) then
AccumulatedCapacity(i,t):= w(i,t)=x(i,t-1)+w(i,t-1);
else
AccumulatedCapacity(i,t):= w(i,t)=x(i,t-1)
end-if
forall(j in Modes,t in 1..T-1)
Demand(j,t):= umd(j,t) + sum(i in Technology) y(i,j,t+1)>=d(j,t+1)
forall(i in Technology,t in 1..T-1)
if(t>=2) then
Capacity(i,t):=sum(j in Modes) y(i,j,t+1)<=(g(i,t)+w(i,t));
else
Capacity(i,t):=sum(j in Modes) y(i,j,t+1)<=g(i,t)
end-if
forall(t in 2..T) OperatingCost(t):=sum(i in Technology,j in Modes)
q(i,t)*tau*y(i,j,t)
minimize(Cost)
writeln(getobjval)
!**************************************************************
procedure generateExhaustiveTree
declarations
E=3 ! Max no. of values, each demand can assume
val,prob:array(Modes,2..T,1..E) of real
end-declarations
initializations from 'CapacityExpansionExhaustive.dat'
val prob
end-initializations
declarations
vals,probs:array(1..E) of real
end-declarations
forall(j in Modes,t in 2..T) do
forall(e in 1..E) do
vals(e):=val(j,t,e)
probs(e):=prob(j,t,e)
end-do
spsetdist(d(j,t),vals,probs)
end-do
spgenexhtree
end-procedure
end-model
Data files:
CapacityExpansion.dat:
r:[464,500,
508,507,
534,490]
q:[.040,.034,.032,
.030,.022,.021,
.019,.018,.016]
g:[80,50,20,
70,35,20,
40,25,15]
tau:2900
Budget:350
Penalty:1300
CapacityExpansionExhaustive.dat:
val:[20,25,0,
28,33,0,
36,40,0,
50,55,0,
58,63,0,
66,70,0,
80,85,0,
88,93,0,
96,100,0]
! replace zeros by some other numbers to get more possible realizations
! andscenarios.
prob:[.5,.5,0,
.5,.5,0,
.4,.6,0,
.6,.4,0,
.4,.6,0,
.6,.4,0,
.4,.6,0,
.5,.5,0,
.5,.5,0]
Stage symmetric model
In order to generate a scenario tree, which is symmetric with respect to stage, the procedure generateExhaustiveTree in the above example can be replaced by the procedure generateStageSymmetricTree which is defined below. The parameter Dep when set to true, would create the tree using the joint probability distribution facility in mmsp.
procedure generateStageSymmetricTree
declarations
NumBranch:array(2..T) of integer
end-declarations
initializations from DIR+"CapacityExpansionStage.dat"
NumBranch
end-initializations
MaxBranch:=max(t in 2..T) NumBranch(t)
declarations
BranchProb:array(2..T,1..MaxBranch) of real
BranchValues:array(Modes,2..T,1..MaxBranch) of real
Prob,Values:array(1..MaxBranch) of real
end-declarations
initializations from DIR+"CapacityExpansionStage.dat"
BranchProb BranchValues
end-initializations
declarations
AllDem:set of sprand
Val:array(Modes,1..MaxBranch) of real
end-declarations
if(Dep) then
forall(t in 2..T) do
AllDem:=union(j in Modes) {d(j,t)}
forall(b in 1..MaxBranch) Prob(b):=0
forall(b in 1..NumBranch(t)) Prob(b):=BranchProb(t,b)
forall(j in Modes,b in 1..MaxBranch) Val(j,b):=0
forall(j in Modes,b in 1..NumBranch(t)) Val(j,b):=BranchValues(j,t,b)
spsetdist(AllDem,Val,Prob)
end-do
spgenexhtree
else
spcreatetree(NumBranch)
forall(t in 2..T) do
forall(b in 1..NumBranch(t)) Prob(b):=BranchProb(t,b)
spsetprobcond(t,Prob)
end-do
forall(t in 2..T,j in Modes) do
forall(b in 1..NumBranch(t)) Values(b):=BranchValues(j,t,b)
spsetrand(d(j,t),Values)
end-do
spgentree
end-if
end-procedure
CapacityExpansionStage.dat:
NumBranch:[8,5,3] BranchProb:[0.15,0.15,0.1,0.1,0.2,0.1,0.1,.1, 0.2,0.2,0.2,0.2,0.2,0,0,0, .25,.5,.25,0,0,0,0,0] BranchValues:[80,81,82,83,84,86,87,88, 86,88,90,93,95,0,0,0, 96,98,100,0,0,0,0,0, 50,51,52,53,54,56,57,58, 56,58,60,63,65,0,0,0, 66,68,70,0,0,0,0,0, 20,21,22,23,24,26,27,28, 26,28,30,33,35,0,0,0, 36,38,40,0,0,0,0,0]
Explicit model
A scenario tree with seven scenarios in the above example can be generated as follows:
procedure generateExplicitTree declarations S=7 ! No. of scenarios A:array(1..S,1..T) of integer ! Node numbers in tree N:array(1..T) of integer ! Number of nodes in each stage end-declarations initializations from DIR+'CapacityExpansionExplicit.dat' A N end-initializations spcreatetree(A) Nmax:=max(t in 1..T) N(t) declarations val:array(2..T,Modes,1..Nmax) of real prob:array(2..T,1..Nmax) of real end-declarations initializations from DIR+'CapacityExpansionExplicit.dat' val prob end-initializations forall(t in 2..T,n in 1..N(t)) spsetprobcondatnode(t,n,prob(t,n)) forall(t in 2..T,j in Modes,n in 1..N(t)) spsetrandatnode(d(j,t),n,val(t,j,n)) spgentree end-procedure
CapacityExpansionExplicit.dat:
A:[1,1,1,1,
1,1,2,2,
1,1,2,3,
1,1,2,4,
1,2,3,5,
1,2,3,6,
1,3,4,7]
N:[1,3,4,7]
val:[20,25,30,0,0,0,0,
50,55,60,0,0,0,0,
30,60,90,0,0,0,0,
25,35,30,30,0,0,0,
55,65,60,60,0,0,0,
85,95,90,90,0,0,0,
38,35,38,40,36,39,38,
68,65,68,70,66,69,68,
98,95,98,100,96,99,98]
prob:[.333,.333,.333,0,0,0,0,
.5,.5,1,1,0,0,0,
1,.333,.333,.333,.5,.5,1]
Results
The results for each of these models with respective scenario generation schemes can be obtained using the standard functions available in the mmsp module and IVE. The plot of other entities, e.g., the operating cost in stage 3, can be viewed in IVE (see Figure Operating cost in third stage (scenario generation scheme: exhaustive)).

Figure 6.5: Operating cost in third stage (scenario generation scheme: exhaustive)
Supply chain management
Consider a supply chain problem in which a company makes products: shirts and trousers and then ships them to different destinations: New York and Los Angeles. The company needs to make production decisions well in advance, and when the demand of each product at each destination occurs, the company needs to make decisions for the next three periods.
Figure 6.6: Products and destinations layout
Model description
- Decisions
- Before demand occurs: How much of each of the products to be bought
- After demand occurs: How much of each of the products to be supplied to each destination
- Constraints
- Available man-hours
- Demand balance constraints
- Objective: Maximize net profit = Expected (Revenue on sales – cost of lost sales – cost of excess supply – cost of procurement)
- Variable xit: Quantity of product i made in the plant at stage t (beginning of tth period)
- Parameter B: Available man-hours at the plant
- Parameter ai: time required on product i
- Variable yijt: Amount of product i supplied to destination j at stage t
- Variables lsijt, esijt: lost sales and excess supply of product i at destination j at stage t.
Demand being a random variable may have a distribution, e.g., as shown below.
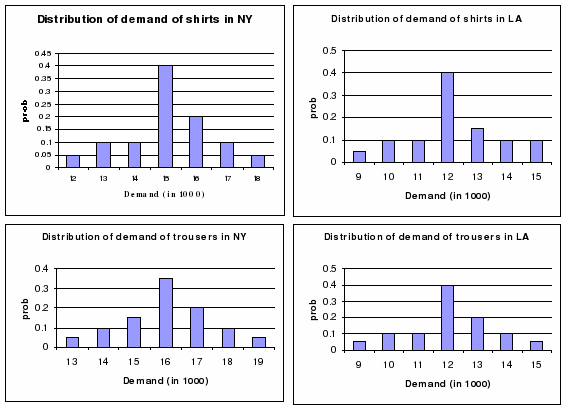
Figure 6.7: Distribution of demand
The company also wants to take into consideration such randomness and hedge against the uncertain future by making an overall optimal decision. The stochastic model looks as follows:
Xpress model
model StochasticMultiStageSupplyChain
uses 'mmsp','mmodbc'
parameters
T=3
DIR=''
end-parameters
declarations
CSTR='DSN=MS Access Database; DBQ='+DIR+'SupplyChain.mdb'
Products,Destinations:set of string
S,CLS,CES: dynamic array(Products,Destinations) of real
C,a: dynamic array(Products) of real
B: real
end-declarations
!--------------------------sets Data Values ----------------------
setparam("SQLverbose",true)
SQLconnect(CSTR)
SQLexecute("select Products,Destinations,SellingPrice, CostOfLostSales,
CostOfExcessSales from DETERMINISTIC_DATA_2INDEX",[S,CLS,CES])
finalize(Products);finalize(Destinations)
SQLexecute("select Products,CostPrice, TimePerUnit from
DETERMINISTIC_DATA_1INDEX",[C,a])
B:=SQLreadreal("select AvailableTime from DETERMINISTIC_DATA_0INDEX")
!--------------------------Stochastic Data values-------------------
declarations
n: array(Products,Destinations) of integer ! number of discretized
! points for distr. of demand
end-declarations
SQLexecute("select Products,Destinations,NoOfDiscretizedPoints from
EXHAUSTIVE_GENERATION_PARAMS", n)
n_max:=max(i in Products,j in Destinations) n(i,j)
declarations
DiscretizedValueDemand,DiscretizedProbabilityDemand:
array(Products,Destinations,1..n_max) of real
end-declarations
SQLexecute("select Products,Destinations,DiscretizedPoint,ValueDemand,
ProbabilityDemand from RANDELEMDISTN", [DiscretizedValueDemand, DiscretizedProbabilityDemand])
SQLdisconnect
!---------------------------- Stochastic Model declarations -----------
setparam('xsp_implicit_stage',true)
declarations
Stages=1..T
x: array(Products,1..T-1) of spvar
y,ls,es: array(Products,Destinations,2..T) of spvar
D: array(Products,Destinations,2..T) of sprand
TotalProfit: splinctr
Time: array(1..T-1) of splinctr
Balance: array(Products,2..T) of splinctr
Demand: array(Products,Destinations,2..T) of splinctr
end-declarations
!---------------------------- Random variables ------------------------
spsetstages(Stages)
declarations
val,prob:array(1..n_max) of real
end-declarations
forall(i in Products,j in Destinations,t in 2..T) do
forall(k in 1..n(i,j)) do
val(k):=DiscretizedValueDemand(i,j,k)
prob(k):=DiscretizedProbabilityDemand(i,j,k)
end-do
spsetdist(D(i,j,t),val,prob)
end-do
spgenexhtree
!---------------------------- Model --------------------------
TotalProfit:= -sum(i in Products,t in 1..T-1) C(i)*x(i,t)+
sum(i in Products,j in Destinations,t in 2..T)
(S(i,j)*y(i,j,t)-CLS(i,j)*ls(i,j,t)-CES(i,j)*es(i,j,t))
forall(t in 1..T-1) Time(t):=sum(i in Products) a(i)*x(i,t)<=B
forall(i in Products,t in 2..T) Balance(i,t):=
sum(j in Destinations) y(i,j,t)=x(i,t-1)
forall(i in Products,j in Destinations,t in 2..T)
if(t>2) then
Demand(i,j,t):=y(i,j,t)+ls(i,j,t)-es(i,j,t)+es(i,j,t-1)=D(i,j,t)
else
Demand(i,j,t):=y(i,j,t)+ls(i,j,t)-es(i,j,t)=D(i,j,t)
end-if
maximize(TotalProfit)
exit(0)
end-model
Data
- DETERMINISTIC_DATA_0INDEX
AvailableTime 165 - DETERMINISTIC_DATA_1INDEX
Products CostPrice TimePerUnit Shirts 10 1 Trousers 20 2 - DETERMINISTIC_DATA_2INDEX
Products Destinations SellingPrice CostOfLostSales CostOfExcessSales Shirts NYC 25 0.75 10 Shirts LA 20 0.25 8 Trousers NYC 45 1.5 15 Trousers LA 40 0.5 15 - EXHAUSTIVE_GENERATION_PARAMS
Products Destinations NoOfDiscretizedPoints Shirts NYC 2 Shirts LA 2 Trousers NYC 2 Trousers LA 2 - RANDELEMDISTN
(consider 2 possibilities for each demand)
Products Destinations DiscretizedPoint ValueDemand ProbabilityDemand Shirts NYC 1 10 0.5 Shirts NYC 2 30 0.5 Shirts LA 1 25 0.5 Shirts LA 2 40 0.5 Trousers NYC 1 30 0.5 Trousers NYC 2 40 0.5 Trousers LA 1 20 0.5 Trousers LA 2 35 0.5
Results
The problem consists of 4096 scenarios. The expected profit is $5,557,731.934. The problem statistics, and the values and distribution of various entities of the model can be viewed in IVE. The figure below shows the distribution of `Total Profit' across the scenarios.

Figure 6.8: Distribution of SP model entity
Option pricing in presence of transaction costs
This model is based on the option pricing model as described in [Cor]. The author assumes a binomial approximation to the Black-Scholes Option Pricing Model to explain the effect of transaction costs on option prices. The behavior of stocks and bonds prices is considered over successive stages. Bonds have fixed annualized rate of return, while stock's prices go up/down depending on the market.
Model description
- Parameters:
- T = Number of stages (indexed by t)
- Assets= {Stocks, Bonds} (indexed by i)
- r = Fixed annualized rate of return of bonds
 = Volatility of returns of stocks
= Volatility of returns of stocks
 = Time span for re-investment
= Time span for re-investment
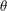 = Transaction cost
= Transaction cost
- X = Strike price of option
- Stochasticity:
 ˜t =
Movement (1/-1 corresponding to up/down) of stock at stage t
˜t =
Movement (1/-1 corresponding to up/down) of stock at stage t- P˜it =
Price of Asset i at stage t:
PBonds,t = PBonds,t-1·er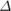 , P˜Stocks,t = P˜Stocks,t-1·e
, P˜Stocks,t = P˜Stocks,t-1·e ˜t
˜t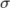 sqrt(
sqrt(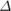 )
)
- Õ =
Option payoff on maturity:
for call option Õ = (P˜Stocks,T - X)+, for put option Õ = (X - P˜Stocks,T)+
- Decision variables:
- qit = Quantity of Asset i at stage t
- xt, yt = Quantity of stocks bought and sold respectively at stage t
- Model formulation:
- minq,x,y
 i
i  Assetsqi,1·Pi,1
Assetsqi,1·Pi,1 - s.t
- qStock,t-qStock,t-1=xt-yt
 t
t {2..T}
{2..T} - (xt(1+
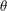 )-yt(1-
)-yt(1- ))·P
))·P Stock,t+ (qBonds,t-qBonds,t)·P
Stock,t+ (qBonds,t-qBonds,t)·P Bonds,t
Bonds,t 0
0  t
t {2..T-1}
{2..T-1} 

i  Assetsi,T-1i,T
Assetsi,T-1i,T O
O
- xt,yt
 0
0 t
t {2..T}
{2..T}
- minq,x,y
Xpress model
model OptionPricing
uses 'mmsp'
parameters
T=5 ! No. of stages
call=true ! Call/ put option
X=100.0 ! Strike price
theta=0.02 ! Fraction of cost of trading
sigma=0.35 ! Volatility
delta=1.0 ! Time-span for re-investment
r=0.07 ! Fixed rate of return for bonds
InitStkPrice=95 ! Stock's price initially
InitBndPrice=100 ! Bond's price initially
end-parameters
forward procedure generate_tree ! Generate tree
declarations
Assets = {"Stocks","Bonds"} ! Set of all the assets
Stages = 1..T !set of stages
q: array(Assets,Stages) of spvar ! Quantity of assets in each stage
x,y: array(2..T) of spvar ! Quant of stocks bought, sold resp
movement: array(2..T) of sprand ! Up/down (1/-1 resp)
price: array(Assets,Stages) of sprandexp ! Price of assets
OptPayOff: sprandexp ! Amount to be paid off at end of horizon
InitInv: splinctr ! Total initial investment
BalanceStocks: array(2..T) of splinctr ! Balance of stocks
BalancePosition: array(2..T) of splinctr ! Balance of cash position
end-declarations
spsetstages(Stages) ! Set stages for SP
setparam('xsp_implicit_stage',true) ! Use last index to associate with stage
forall(t in Stages) ! Random price of assets in each stage
if t=1 then
price("Stocks",t):=InitStkPrice
price("Bonds",t):=InitBndPrice
else
price("Stocks",t):=price("Stocks",t-1)*exp(movement(t)*sigma*delta^0.5)
price("Bonds",t):=price("Bonds",t-1)*exp(r*delta)
end-if
if call then ! payoff at end depending on option type
OptPayOff:=maximum(price("Stocks",T)-X,0)
else
OptPayOff:=maximum(X-price("Stocks",T),0)
end-if
generate_tree ! Generate stoch. tree based on movement
forall(i in Assets,t in Stages)
q(i,t) is_free ! Negative value implies short position
InitInv:=sum(i in Assets) q(i,1)*price(i,1)
forall(t in 2..T)
BalanceStocks(t):= q("Stocks",t)-q("Stocks",t-1) = x(t)-y(t)
forall(t in 2..T)
if t=T then
BalancePosition(t):= sum(i in Assets) q(i,t-1)*price(i,t) >= OptPayOff
else
BalancePosition(t):=
(x(t)*(1+theta)-y(t)*(1-theta))*price("Stocks",t)+
(q("Bonds",t)-q("Bonds",t-1))*price("Bonds",t) <= 0
end-if
setparam("xsp_scen_based",false) ! Create a node based problem
minimize(InitInv)
!*****************************************************************
procedure generate_tree
declarations
val:array(1..2) of real
prob:array(1..2) of real
end-declarations
val:=[1,-1] ! Up/down movement values
prob:=[.5,.5] ! Up/down movement probabilities
forall(t in 2..T) spsetdist(movement(t),val,prob) ! Set distribution
spgenexhtree ! Generate exh. tree based on distrib.s
end-procedure
end-model
Results
The model is solved by varying the value of
![]() from 0 to 0.1.
from 0 to 0.1.

From the above figure it can be observed that as the transaction cost is increased, the initial investment also increases almost linearly. Additionally, with the increase in transaction cost, the initial quantity of stocks bought keeps increasing, while the quantity of bonds that is kept on a short position keeps decreasing. Other results may be analyzed using IVE.
Airlift operations scheduling model
This model is based on the airlift operation scheduling problem described by Ariyawansa and Felt in their collection of stochastic linear programming test problems [AF05]. The problem consists of scheduling airlift operations along a set of routes during a period of one month. The demands of routes can be predicted but are subject to changes. A random variable is assigned for each demand. If the predicted demands do not agree with the actual demands, a recourse action is taken.
To meet the route demands, several types of aircrafts are available. Each aircraft has its own characteristics, namely availability of number of flight hours per month and carrying capacity when flying a specific route.
The recourse actions that can be taken are to switch aircrafts from one route to another, to leave some flights unused, and to contract commercial flights to meet the demands of routes.
Let aij be the number of hours required by an aircraft of type i to complete a flight of route j and let xij be the number of flights planned for route j using aircraft of type i and the maximum number of flight hours for aircraft of type i during a month. Then, the constraint on the number of flight hours used by an aircraft of type i during the month is
Let aijk be the number of hours required by an aircraft of type i to fly route k after having been switched from route j and let xijk be the increase of flights in route k after switching an aircraft i from route j. Then we have the following constraint that states that the number of flight hours switched from an aircraft of type i and from route j is at most the amount we have originally scheduled:
Let the carrying capacity of aircraft of type i when flying in route j be denoted by bij, the demand of route j commercially contracted in the recourse by yj+, and the unused capacity assigned to route j by. We can express a constraint that ensures that the flight hours initially scheduled for route j, the flights switched from and to route j, the commercially contracted demand, and the unused capacity sum up to the demand dj of route j as follows:
| aijk |
| aij |
Let cij be the cost of initially assigning an aircraft of type i to fly one flight on route j, and let cijk be the cost for aircraft of type i to fly one flight of route k after having been switched from route j. With cj+ denoting the cost of transporting one unit of demand of route j by a commercially contracted flight and denoting the cost of one unit of unused capacity on route j, we can define the model as follows:

The following table describes the constraints of the model, the data, and the decision variables (with its corresponding names in the Mosel code).
| Identifier | Meaning |
|---|---|
| aij (A) | number of hours required by aircraft of type i to complete a flight of route j |
| aijk (Aswitch) | as the number of hours required by aircraft of type i to fly route k after having been switched from route j |
| xij (x) | number of flights planned for route j using aircraft of type i |
| xijk (xswitch) | increase of flights in route k after switching aircraft i from route j |
| Fi (F) | maximum number of flight hours for aircraft of type i during a month |
| cij (Cost) | cost of initially assigning aircraft of type i to fly one flight of route j |
| cijk (CostSwitch) | cost for aircraft of type i to fly one flight of route k after having been switched from route j |
| cj+ (cplus) | cost of transporting one unit of demand of route j by a commercially contracted flight |
| cj- (cminus) | cost of one unit of unused capacity on route j |
| yj+ (yplus) | demand of route j commercially contracted in the recourse |
| yj- (yminus) | unused capacity assigned to route j |
| bij (b) | carrying capacity of aircraft of type i when flying in route j |
| dj (d) | demand of route j |
| MaxHours(i) | constraints (1) of the model |
| MaxSwitch(i,j) | constraints (2) of the model |
| DemandCtr(j) | constraints (3) of the model |
| ExpTotalCost | objective function |
Implementation
Below, we show the Mosel code that implements the model and solves it using Xpress-SP.
model airlift
uses "mmsp"
parameters
DIR="."
end-parameters
declarations
NAIRCRAFTS = 2
NROUTES = 2
SCEN = 25
AIRCRAFTS = 1..AIRCRAFTS
ROUTES = 1..NROUTES
A : array(AIRCRAFTS,ROUTES) of integer
Aswitch : array(AIRCRAFTS,ROUTES,ROUTES) of integer
F : array (AIRCRAFTS) of integer
b : array (AIRCRAFTS,ROUTES) of integer
Cost : array (AIRCRAFTS,ROUTES) of real
CostSwitch: array (AIRCRAFTS,ROUTES,ROUTES) of real
cplus : array (ROUTES) of real
cminus : array (ROUTES) of real
Probabilities : array (1..SCEN) of real
DValues : array (ROUTES,1..SCEN) of real
d : array (ROUTES) of sprand
MaxHours : array (AIRCRAFTS) of splinctr
MaxSwitch : array (AIRCRAFTS, ROUTES) of splinctr
DemandCtr : array (ROUTES) of splinctr
x : array (AIRCRAFTS,ROUTES) of spvar
xswitch : dynamic array (AIRCRAFTS,ROUTES,ROUTES) of spvar
yplus : array (ROUTES) of spvar
yminus : array (ROUTES) of spvar
end-declarations
! Read data
initializations from DIR+'airlift.dat'
A Aswitch F b Cost CostSwitch
cplus cminus DValues Probabilities
end-initializations
!---------------------------------------------------------
! Create scenario tree
declarations
Stages = {"First","Recourse"}
Branches: integer
Values : array (1..SCEN) of real
end-declarations
spsetstages(Stages)
forall(i in ROUTES) spsetstage(d(i),"Recourse")
spcreatetree(SCEN)
spsetprobcond(2,Probabilities)
forall(i in ROUTES, j in 1..SCEN) spsetrandatnode(d(i),j,DValues(i,j))
spgentree
!---------------------------------------------------------
forall (i in AIRCRAFTS, j in ROUTES, k in ROUTES | k<>j)
create(xswitch(i,j,k))
ExpTotalCost :=
sum(i in AIRCRAFTS, j in ROUTES) Cost(i,j)*x(i,j) +
sum(i in AIRCRAFTS, j in ROUTES, k in ROUTES | k<>j)
(CostSwitch(i,j,k) - Cost(i,j)*Aswitch(i,j,k)/A(i,j))*xswitch(i,j,k)+
sum(j in ROUTES) cplus(j)*yplus(j) +
sum(j in ROUTES) cminus(j)*yminus(j)
! First stage constraints:
forall (i in AIRCRAFTS)
MaxHours(i):= sum(j in ROUTES) A(i,j)*x(i,j) <= F(i)
! Second stage constraints:
forall (i in AIRCRAFTS, j in ROUTES)
MaxSwitch(i,j):=
sum(k in ROUTES | k<>j) Aswitch(i,j,k)*xswitch(i,j,k)
<= A(i,j)*x(i,j)
! Demand constraint for recourse
forall (j in ROUTES)
DemandCtr(j):= -sum(i in AIRCRAFTS,k in ROUTES | k<>j)
(b(i,j)*Aswitch(i,j,k)/A(i,j))*xswitch(i,j,k) +
sum(i in AIRCRAFTS,k in ROUTES | k<>j)
b(i,j)*xswitch(i,k,j) +
yplus(j) - yminus(j) =
d(j)- sum(i in AIRCRAFTS) b(i,j)*x(i,j)
! Associate spvars to stages
forall(i in AIRCRAFTS,j in ROUTES) spsetstage(x(i,j),'First')
forall(i in AIRCRAFTS,j in ROUTES,k in ROUTES | k<>j)
spsetstage(xswitch(i,j,k),'Recourse')
forall(j in ROUTES) spsetstage(yplus(j),'Recourse')
forall(j in ROUTES) spsetstage(yminus(j),'Recourse')
! Set variables as integer
forall(i in AIRCRAFTS,j in ROUTES) x(i,j) is_integer
forall(i in AIRCRAFTS,j in ROUTES,k in ROUTES | exists(xswitch(i,j,k)))
xswitch(i,j,k) is_integer
setparam('xprs_cutfreq', 1)
setparam('xprs_cutdepth', 40)
setparam('xprs_treegomcuts', 1)
setparam('xprs_varselection', 3)
minimize(ExpTotalCost)
writeln(getobjval)
end-model
Results
Here, we present results for a small example, with two types of aircrafts, two routes and twenty-five scenarios. The expected total cost is $229,431. The values of the variables xij and xijk are shown in the figure below for a specific scenario (scenario 7). The solution is shown in the following picture, where A-B corresponds to route 1 and C-D to route 2. The pairs (a,b) give the number of aircrafts of type 1 and 2, respectively, that are initially assigned to each route. The pairs [a,b] give the number of aircrafts of type 1 and 2 respectively, that are switched from one route to another in the recourse stage, depending on the direction of the arrow.
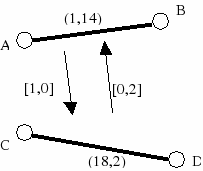
Figure 6.9: Schedule
The data file airlift.dat is shown in the Appendix. Figure Airlift model in Xpress-IVE. shows the model and its associated scenario tree in Xpress-IVE.

Figure 6.10: Airlift model in Xpress-IVE.
Analysis
An interesting way of measuring the quality of the stochastic solution of model airlift is to compare its result to that of the expected value version of the model. To solve the expected value problem in Xpress-SP the model shown above can be used. The only difference is that when optimizing, the type of problem that must be solved is specified:
minimize(ExpTotalCost,XSP_EV+XSP_REC) ! Expected value with recourse
The expected value version of the model has an optimal objective function value of $237,016. Thus, the value of the stochastic solution is
Other useful techniques that can be easily applied in Xpress-SP
consist of scenario aggregation and deletion. For instance, one may
want to delete/aggregate scenarios that are unlikely to happen and
some scenarios that describe similar realizations. In these
situations, it may be interesting to delete scenarios or aggregate
some of them, in order to simplify the problem. This task can be
performed using Xpress-IVE using the Run options
window of Xpress-IVE (Menu Build ![]() Options). The option `Pause
to prune scenario tree manually' allows the user to select
some scenarios (as show in Figure Pruning scenario tree in Xpress-IVE.), delete them, and resume
execution, in which case the problem is solved with the current
scenario tree. Aggregation can be done in a similar way.
Options). The option `Pause
to prune scenario tree manually' allows the user to select
some scenarios (as show in Figure Pruning scenario tree in Xpress-IVE.), delete them, and resume
execution, in which case the problem is solved with the current
scenario tree. Aggregation can be done in a similar way.
As an example, suppose that the user decides to delete the scenarios related to the lowest demand predictions. If we delete the seven scenarios with lowest demands for the second route (by using the procedure spdelscen({2,8,9,10,12,18,23})), we end up with a problem with 18 scenarios, which gives expected total cost $233,389. If we do a similar exercise, but removing the 7 scenarios with highest demand prediction for the second route (spdelete({1,3,7,11,13,14,20})), we have an expected total cost equal to $222,258.

Figure 6.11: Pruning scenario tree in Xpress-IVE.
Forest planning
This model is based on the forest planning problem described by Ariyawansa and Felt in their collection of stochastic linear programming problems [AF05]. The goal is to maximize the value of timber, both cut and remaining, after the last period of planning. The constraints in this model pertain to the amount of forest cut in a single period, the age of trees, and the likelihood that trees remaining uncut are destroyed by fire.
Each tree belongs to one of K age classes of equal length. The length that defines the age classes is also used to define the length of stages of the planning period. Thus, trees belonging to age class A in a given stage will belong to age class A+1 in the next stage if they are not cut or destroyed by fire. Whenever any of these events take place, new trees are planted and, the number of trees in the first age class equals the sum of these two quantities.
The variables of the model are the total area of forest for each age class, for each period (vector st), the amount of forest harvested for each age class in each period (vector xt), and penalty factors for not satisfying constraints on the amount of harvested area in each period (vectors pt1 and pt2).
A natural constraint is one that restricts the harvested area to be at most the total amount of area for each age class in each period t = 1,...,T:
The next set of constraints on the harvested area involve penalty factors pt1 and pt2 which try to avoid the harvested quantities exceeding limits of how fast the timber industry can change its purchasing volume from the current period to the next:
yTxt-1 -
In these constraints ![]() and
and ![]() are constants and y is a vector representing the yield of
selling one unit of harvested area of each class.
are constants and y is a vector representing the yield of
selling one unit of harvested area of each class.
The matrices Q and Pt shown below are square matrices of dimension K that are used to express the total number of trees in each period for each age class, taking into account both harvesting and fire in the previous stage.


Thus, the following constraint expresses the total area in the beginning of period t, for t = 2,...,T:
Below, we describe the complete model.
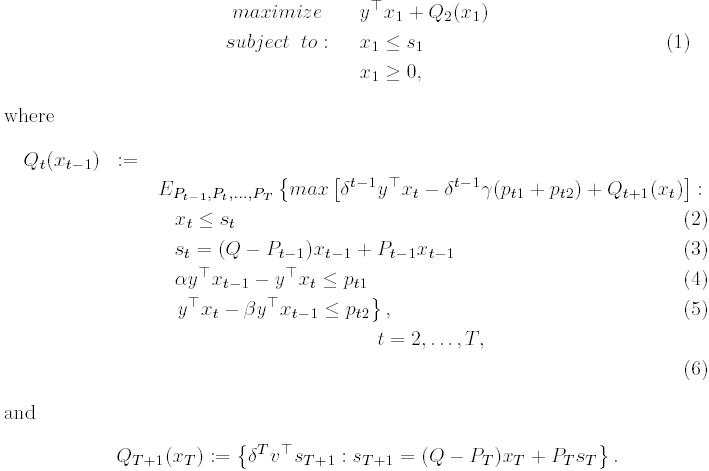
In this model ![]() is a factor used to discount monetary values and depends on the
inflation rate and the size of the planning period, v
is a vector with the values of the trees in each age class, standing
after the last period, and
is a factor used to discount monetary values and depends on the
inflation rate and the size of the planning period, v
is a vector with the values of the trees in each age class, standing
after the last period, and ![]() is a constant penalty factor. The objective function is to maximize
the expected total profit.
is a constant penalty factor. The objective function is to maximize
the expected total profit.
The following table describes the constants, data, decision variables, and constraints of the model (with its corresponding names in the Mosel code).
| Identifier | Meaning |
|---|---|
| constants of the model (read from data file) | |
| y (yield) | yield of selling an unit of harvested area |
| v (v) | value of the trees standing after the last period |
| xt (x) | amount of harvested forest of each age class in each period |
| st (s) | total area of forest of each age class in each period |
| pt1 (p1) | penalty variable for not satisfying constraints YlowerLimit |
| pt2 (p2) | penalty variable for not satisfying constraints YUpperLimit |
| P | matrix of sprands representing the probabilities of fire |
| ProbDiscret | probability discretization of the realization of each fire probability |
| ValuesDiscret | fire probability for each period |
| HarvestLimit | constraints (1) and (2) in the model |
| Fix | auxiliar constraint that fixes s1 variables |
| s1 | auxiliary data for fixing s1 (initial planted area) |
| TotalArea | constraints (3) in the model |
| YlowerLimit | constraints (4) in the model |
| YupperLimit | constraints (5) in the model |
Below, we show the Mosel code that implements the model and solves it in Xpress-SP. The matrices Q and Pt are not stored explicitly as matrices. Instead, constraints (3) of the model are generated based on the structure of both matrices using the sprand P, as can be seen in the Mosel code for constraints TotalArea.
model forest_relax
uses "mmsp"
parameters
EPS = 1e-5
end-parameters
declarations
T=7
K=8
MAXDISCRET=3
AGES = 1..K
index:integer
alpha,beta,delta,gama: real
ScenariosAgg,ScenariosDel: set of integer
yield, v: array (AGES) of real
ProbDiscret,ValuesDiscret: array(1..MAXDISCRET, 1..MAXDISCRET) of real
s1: array (AGES) of real
end-declarations
declarations
P: array (AGES, 2..T+1) of sprand
x: array (AGES, 1..T) of spvar
s: array (AGES, 1..(T+1)) of spvar
p1,p2: array (2..T) of spvar
HarvestLimit: array (AGES, 1..T) of splinctr
Fix: array (AGES) of splinctr
TotalArea: array (AGES, 2..(T+1)) of splinctr
YLowerLimit: array (2..T) of splinctr
YUpperLimit: array (2..T) of splinctr
end-declarations
! Read data
initializations
from 'forest.dat'
yield
v alpha beta delta gama
ProbDiscret
ValuesDiscret s1
end-initializations
! Create scenario tree
declarations
Stages = 1..(T+1)
Branches: array (1..T) of integer
Probabilities: array (1..MAXDISCRET) of real
PValues: array (1..MAXDISCRET) of real
end-declarations
spsetstages(Stages)
forall(t in 2..T+1, i in AGES) spsetstage(P(i,t), t)
Branches:= [1, 3,3,3, 3,3,3]
spcreatetree(Branches)
forall(t in 2..T+1) do
forall(i in 1..MAXDISCRET) PValues(i):= ValuesDiscret(Branches(t-1),i)
forall(i in AGES) spsetrand(P(i,t), PValues)
end-do
forall(t in 1..T) do
forall(i in 1..MAXDISCRET)
Probabilities(i):= ProbDiscret(Branches(t),i)
spsetprobcond(t+1,Probabilities)
end-do
setparam('xsp_scen_based', false)
spgentree
! Objective function
ObjFnc:= sum(t in 1..T, i in AGES) (delta^(t-1))*yield(i)*x(i,t) +
sum(i in AGES)(delta^T)*v(i)*s(i,T+1) -
gama*sum(t in 2..T) (delta^(t-1))*(p1(t) + p2(t))
! Spvars s(T+1) should be associated to stage T
! Constraints
forall(j in AGES, t in 1..T) HarvestLimit(j,t):= x(j,t) <= s(j,t)
forall(j in AGES) Fix(j):= s(j,1) = s1(j)
forall(i in AGES, t in 2..(T+1))
if i=1 then
TotalArea(i,t):= s(i,t) = sum(j in AGES) (1 -P(j,t))*x(j,t-1) +
sum(j in AGES) P(j,t)*s(j,t-1)
elif i=K then
TotalArea(i,t):= s(i,t) = -(1-P(K-1,t))*x(K-1,t-1) -
(1-P(K,t))*x(K,t-1) +
(1-P(K-1,t))*s(K-1,t-1) +
(1-P(K,t))*s(K,t-1)
else
TotalArea(i,t):= s(i,t) = -(1 - P(i-1,t))*x(i-1,t-1) +
(1 - P(i-1,t))*s(i-1,t-1)
end-if
forall(t in 2..T) do
YUpperLimit(t):= - sum(j in AGES) yield(j)*x(j,t) +
alpha*sum(j in AGES) yield(j)*x(j,t-1) <= p1(t)
YLowerLimit(t):= sum(j in AGES) yield(j)*x(j,t) -
beta*sum(j in AGES) yield(j)*x(j,t-1) <= p2(t)
end-do
! Associate Spvars to stages
forall(t in 1..T, i in AGES) do
spsetstage(x(i,t),t)
spsetstage(s(i,t),t)
end-do
forall(i in AGES) spsetstage(s(i,T+1),T)
forall(t in 2..T) do
spsetstage(p1(t),t)
spsetstage(p2(t),t)
end-do
setparam('xsp_verbose', true)
! Optimize
maximize(ObjFnc)
end-model
Note that an alternative structure of the scenario tree (different discretization) can be evaluated by changing the corresponding line of the Mosel code. For example, a tree with 3 branches at each stage may describe the problem more accurately and can be set by the statement Branches:= [1, 3,3,3, 3,3,3].
For the data we are using in the Appendix, the maximum number of branches (MAXDISCRET) in a node is 3. However, if the user provides the probabilities and the values of the corresponding sprand in the datafile, the branching structure can naturally be expanded to more than 3 branches.
Results
Running the model with the data provided in the Appendix gives the expected total profit of $4.23004e+007. This value is obtained for the problem when considering the structure of the scenario tree given by the statement Branches:= [1, 2,3,2, 2,2,2].
Analysis
The expected value version of the model has an optimal profit value of $4.21329e+007. The model is optimized with the following Mosel statement:
maximize(ObjFnc, XSP_EV+XSP_REC) ! Expected value with recourse
The value of the stochastic solution is of the order
The perfect information version is solved by calling maximize as follows:
maximize(ObjFnc, XSP_PI) ! Perfect information problem
This gives a profit of $4.51233e+007 and the value for the perfect information solution equal to
In all three problems, the only nonzero first stage variable is x(1,8), that is associated to the last age class. Below, we show a table with the value of x(1,8) in the three problems:
| Problem | Value of x(1,8) | Objective Function |
|---|---|---|
| Recourse | 20516.9 | 4.23004e+007 |
| Expected value | 20738.7 | 4.21329e+007 |
| Perfect information | 19770.3 | 4.51233e+007 |
Suppose that after solving the model the user wants to remove scenarios that give low values for the objective function. Below, we show an additional Mosel code that makes use of the routines speval and spdelscen to inspect the objective function value (profit) associated with each scenario. The scenarios where the objective function values are less than 95% of the optimal value for the stochastic problem are removed and the problem is solved again. Using this policy, the user iteratively removes scenarios until the objective function in all scenarios is greater than 95% of the new optimal objective function value.
Scenarios:= 1
forall(t in 1..T) Scenarios *= Branches(t)
while(true) do
ScenariosDel:= {}
forall(sce in 1..Scenarios| speval(ObjFnc,scen)<0.95*getobjval)
ScenariosDel+= {scen}
if (getsize(ScenariosDel)=0) then
break
end-if
spdelscen(ScenariosDel)
Scenarios -= getsize(ScenariosDel)
maximize(ObjFnc)
writeln(getobjval)
end-do
The variable ScenariosDel is a set of integers that specifies the scenarios that will be deleted. The table below shows the objective function value for the stochastic problem at each iteration of this procedure, until there are no such scenarios to be removed.
| Iteration | Expected total profit |
|---|---|
| 0 | 4.22529e+007 |
| 1 | 4.22907e+007 |
| 2 | 4.22990e+007 |
| 3 | 4.23034e+007 |
| 4 | 4.23041e+007 |
| 5 | 4.23072e+007 |
| 6 | 4.23096e+007 |
Iteration 0 refers to the objective function value of the original stochastic problem. The original problem had 729 scenarios and the final problem solved at iteration 6 had 675 scenarios. The scenario tree for this problem is generated by using the branching scheme Branches:= [1, 3,3,3, 3,3,3].
It is also possible to make a similar exercise, aggregating scenarios that have low probability by using the routines spgetscenprob and spaggregate. The following code aggregates scenarios that have probability less than 0.1% and are contiguous in the scenario tree, with the same parent node. After aggregation, we end up with 480 scenarios and expected total profit $4.2484e+007.
Scenarios:= 1
forall(t in 1..T) Scenarios *= Branches(t)
ScenariosAgg:= {}
forall(scen in 1..Scenarios | spgetprobscen(scen)<0.001)
ScenariosAgg+= {scen}
scen:= getsize(ScenariosAgg)
AggOcurred:= false
while(scen >= 1) do
siblings:= {ScenariosAgg(scen)}
forall(j in 1..(MAXDISCRET-1) | scen-j>0 ) do
if (ceil(ScenariosAgg(scen-j)/Branches(T)) =
ceil(ScenariosAgg(scen)/Branches(T))) then
siblings+= {ScenariosAgg(scen-j)}
else
break
end-if
end-do
if (getsize(siblings)>1) then
writeln('aggregating ', siblings)
spaggregate(siblings)
AggOcurred:= true
end-if
Scenarios -= getsize(siblings) + 1
scen -= getsize(siblings)
end-do
maximize(ObjFnc)
writeln(getobjval)
The set ScenariosAgg is a set of integers that specifies the scenarios with probability less than 0.1%. From ScenariosAgg, we select the scenarios to be aggregated by checking if they have the same parent in stage 7. This task is done by using the information on the number of branches in stage 7:
ceil(ScenariosAgg(scen)/Branches(T))
Below, we show a table that presents the differences between the node-based version and the scenario-based version of this model, in terms of number of rows and columns. The values are shown before and after pre-solving takes place, for the problem with 729 scenarios.
| Before presolve | After presolve | |||
|---|---|---|---|---|
| Rows | Columns | Rows | Columns | |
| Node Based | 12400 | 8512 | 7922 | 5885 |
| Scenario Based | 183944 | 96228 | 4479 | 3758 |
Summary
In this section, we have just shown some of the features, embedded in Xpress-SP, that allow the user to optimize stochastic problems and perform further analysis in an easy and customizable way: by inspecting variables in particular scenarios, aggregating/deleting scenarios, obtaining estimates from the expected value and perfect information problems, and choosing among different ways of expanding the problem. These ideas play an important role in providing insight into the problem and simplifying or strengthening its formulation.
Assets and liabilities management for pension funds
Assets and liabilities management (ALM) problems are one of the most important classes of problems arising in the financial area. Typically the goal of these problems is to find an optimal strategy for allocating resources in order to obtain a profit that is sufficient to cover a certain type of liability. These problems often involve uncertain parameters; for instance, the returns received from different investments usually depend on unknown future market conditions. The amounts of liabilities that need to be paid at certain time can also depend on various future factors. Therefore, in many cases, applying stochastic programming techniques is crucial for making strategic decisions that efficiently handle the risk of possible losses.
We consider one of the practically important instances of these problems — assets and liabilities management for pension funds. A typical pension fund has members that can be separated into two classes. The first class is `active members', i.e., employees paying a certain fraction of their wages to the pension fund each month. The second class is `non-active' members, i.e., people who have retired and receive payments from the pension fund. At every time period the pension fund should have enough assets to be able to cover all the payments (liabilities). The problem the pension fund manager is faced with is minimizing the contribution rate (fraction of wages) paid by the active members while being able to cover the liabilities. The setup of the problem aims to ensure that the percentage of wages that the employees pay is small enough to attract new pension fund members. To cover the liabilities, assets owned by the fund are invested into stocks, whose returns are uncertain. Moreover, the amount of liabilities is also uncertain, since it depends on the inflation rate and demographic factors. Stochastic programming techniques allow one to expand the deterministic formulation of the model by using scenario data for uncertain parameters.
First, we present the formal setup of the model. These are its parameters, decision variables, and the deterministic formulation (assuming that all the parameters are known and no uncertainty is involved). Here we consider the one-period model, i.e., there is only one planning period, where the investment decision is made at the initial moment in order to cover the liabilities at the end of the period.
Parameters of the model
A0
– the initial value of all assets owned by the fund.
W0
– the total amount of wages of the active members at the
initial moment.
l0
– the payments made by the fund at the initial moment.
rn
– the rate of return of the stock number n, n = 1, ..., N.
L –
the liability measure that should be exceeded by the total value of
assets at the end of the period.
![]() – the
parameter used to control the behavior of the fund. We want the
total return to exceed the liabilities by a certain amount, for
instance, if
– the
parameter used to control the behavior of the fund. We want the
total return to exceed the liabilities by a certain amount, for
instance, if ![]() = 1.3
then we want the total return to be at least 30% higher than the
liabilities.
= 1.3
then we want the total return to be at least 30% higher than the
liabilities.
Decision variables
xn
– the total amount of money invested in the stock number
n, n = 1, ..., N.
y –
the contribution rate (fraction of wages) that is added to the
initial assets at the initial time moment.
Deterministic problem formulation
Z=miny ![]() R, x
R, x ![]() RNy
RNy
![]()
=A0-l0+W0y
N
n=1n
![]()
N
n=1nn
![]()
![]() L
L
xn![]() 0
0 ![]() n
n ![]() {1..N}
{1..N}
Description
The first constraint is the investment balance: the total money invested in the stocks xn should be equal to the total assets available at the beginning of he period, i.e., the initial assets plus the fraction of wages paid by active members minus payments made at the beginning of the period.
The second constraint expresses the fact that the total return at the end of
the period must exceed the amount of liabilities (multiplied by the
control parameter ![]() ).
).
The third set of constraints is the non-negativity constraints on xn that means that we don't allow any `short' positions or borrowing. Note that we don't impose any restrictions on y, we allow it to be negative. If y is negative, it means that the fund can cover all the liabilities without taking money from active members and even make additional payments to them.
Stochastic problem formulation
We now consider the ALM problem with N = 12 stocks and S = 5000 scenarios corresponding to the realizations of the returns and liabilities. We create the scenario tree based on the real-life data representing returns of 12 stocks, as well as the amount of liabilities. This tree has two stages and 5000 nodes at the second stage. Certain realizations of the returns and liabilities correspond to each node at the second stage. The probabilities of all realizations are assumed to be the same and equal to P = 1/S.
The extended two-stage formulation of the problem can be written as follows:
Z=miny ![]() R, x
R, x ![]() RNy
RNy
![]()
=A0-l0+W0y
N
n=1n
![]()
Ns
n=1nn
![]()
![]() Ls
Ls ![]() s
s ![]() {1..S}
{1..S}
xn![]() 0
0 ![]() n
n ![]() {1..N}
{1..N}
Mosel implementation
Using stochastic modeling tools in Mosel, one can create the scenario tree representing stochastic parameters of the model and specify the constraints of the deterministic model then the extended (stochastic) problem formulation is generated automatically. The Mosel implementation of the stochastic model is presented below.
model ALM_sp
uses 'mmsp' ! Use the stochastic programming module
parameters
psi=1.3
end-parameters
declarations
Stocks=1..12 ! Set of stocks
Intial_Asset,A: real
Initial_payment,l: real ! Payments at the initial time
Total_wages,W: real ! Total amount of wages of active members
! of the fund
end-declarations
! Initial (deterministic) parameters
initializations from 'ALM.dat'
Intial_Asset Initial_payment Total_wages
end-initializations
A:=1 ! Scaled value of initial assets
l:=Initial_payment/Intial_Asset ! Scaled value of initial payments
W:=Total_wages/Intial_Asset ! Scaled value of wages
declarations
Stages = {"First","Second"} ! Two stages - one-period model
! Random parameters
return: array(Stocks) of sprand ! Uncertain returns of the stocks
L: sprand ! Uncertain liabilities
! Decision variables
x: array(Stocks) of spvar ! Amount invested into each stock
y: spvar ! % of wages paid by active members
! Model objective and constraints
fraction: splinctr
inv_balance: splinctr
minreturn: splinctr
end-declarations
! Allow contribution rate to be both positive and negative
y is_free
! Setting stages
spsetstages(Stages)
forall(p in Stocks) spsetstage(return(p),"Second")
spsetstage(L,"Second")
! Scenarios declaration and generating scenario tree
declarations
S = 500
Scen = 1..S
Values: array(Scen, Stocks) of real
Liab: array(Scen) of real
end-declarations
spcreatetree(S)
forall(s in Scen) prob(s):=1/S
spsetprobcond(2,prob)
initializations from 'returns.dat'
Values
end-initializations
initializations from 'Liabilities.dat'
Liab
end-initializations
forall(p in Stocks,s in Scen) spsetrandatnode(return(p),s,Values(s,p))
forall(s in Scen) spsetrandatnode(L,s,Liab(s)/Intial_Asset)
spgentree
! Model definition
fraction:= y
inv_balance:=sum(p in Stocks)1*x(p) = A - l + W*y
minreturn:=sum(p in Stocks)(1+return(p))*x(p) >= psi*L
! Assigning variables to stages
forall(p in Stocks) spsetstage(x(p),"First")
spsetstage(y,"First")
! Optimizing
minimize(fraction)
! Solution output
writeln("psi = ", psi)
writeln("contribution rate = ", getobjval)
forall(p in Stocks) writeln("x(", p, ") = ", getsol(x(p)))
end-model
Note that for convenience the monetary parameters of the model are scaled, i.e., divided by the amount of the initial assets A0. The description of the data files data.dat and data_L.dat used for generating the scenario tree can be found in the Appendix. The expected value (ZEV) and perfect information (ZPI) solutions can be found by running this program after modifying the line minimize(fraction) by minimize(fraction,XSP_EV) and minimize(fraction,XSP_PI) respectively.
Analysis of the results
Table Optimal objective values for different
values of .
(see Appendix) presents the values of the objective
function (i.e., contribution rate) for the original stochastic
problem (Z*), and for the expected value and perfect
information problems, for different values of the control parameter
![]() . The differences
between these solutions are also calculated.
. The differences
between these solutions are also calculated.
An interesting observation is that all these solutions, as well as the
differences Z*- ZEV and Z*- ZPI are linear functions of ![]() (see Figure Linear dependency of the optimal solutions ). Linear dependency of Z*, ZEV
and ZPI of
(see Figure Linear dependency of the optimal solutions ). Linear dependency of Z*, ZEV
and ZPI of ![]() can be easily proven theoretically, using LP sensitivity analysis
techniques. Since Z*, ZEV and ZPI
are linear functions of
can be easily proven theoretically, using LP sensitivity analysis
techniques. Since Z*, ZEV and ZPI
are linear functions of ![]() ,
the differences Z*- ZEV and Z*- ZPI
representing the `value' of deterministic solution and
perfect information are also linear with respect to
,
the differences Z*- ZEV and Z*- ZPI
representing the `value' of deterministic solution and
perfect information are also linear with respect to ![]() .
Note that the optimal stochastic solution is much larger than the
corresponding expected value and perfect information solutions,
which means that one is forced to take more conservative decisions
(i.e., spend more money) if uncertainty is taken into account. Also,
as
.
Note that the optimal stochastic solution is much larger than the
corresponding expected value and perfect information solutions,
which means that one is forced to take more conservative decisions
(i.e., spend more money) if uncertainty is taken into account. Also,
as ![]() increases, the
values Z*- ZEV and Z*- ZPI
also increase, which means that the stochastic solution becomes
more `expensive' if a greater amount of liabilities
needs to be covered.
increases, the
values Z*- ZEV and Z*- ZPI
also increase, which means that the stochastic solution becomes
more `expensive' if a greater amount of liabilities
needs to be covered.
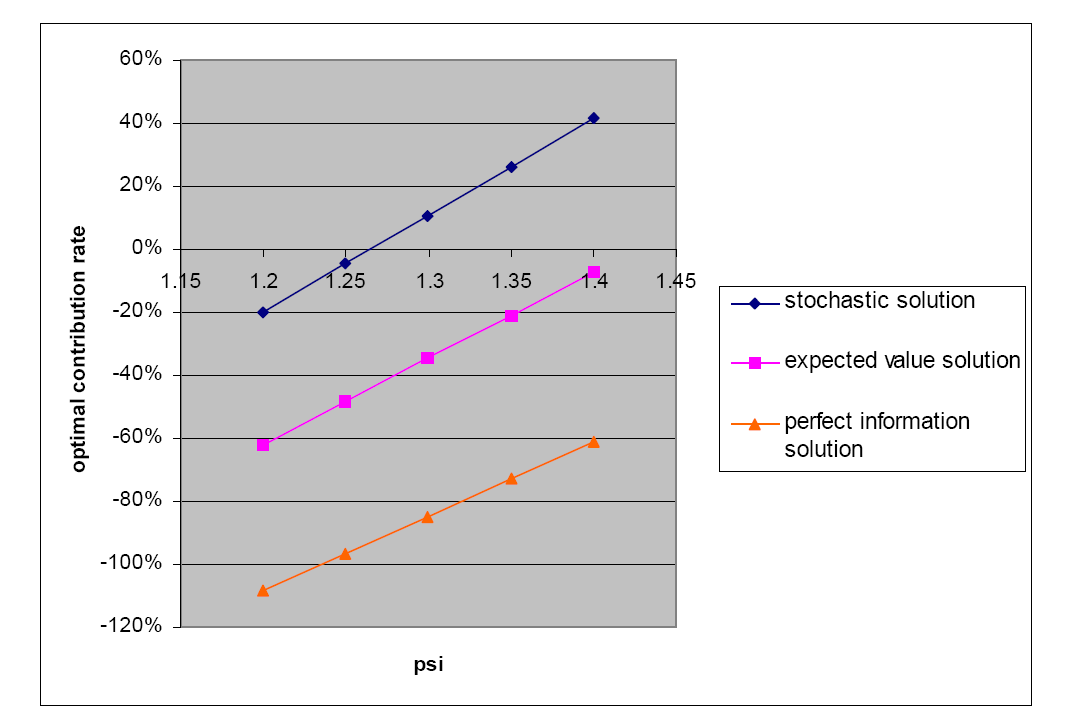
Figure 6.12: Linear dependency of the optimal solutions w.r.t. ![]() .
.
It is also important to look at the optimal investment strategy found
from solving the stochastic problem. As one can see from Table Investment decisions (scaled values) for
different values of .
(see Appendix), the relative structure of the investments remains
the same for all considered ![]() 's,
however, the amounts invested into each stock increase as
's,
however, the amounts invested into each stock increase as ![]() increases.
increases.
Another issue that we address here is how the structure of the scenario
dataset affects the optimal solution of the stochastic problem. For
this purpose, we calculated the mean ![]() n
and the standard deviation
n
and the standard deviation ![]() n
of the return of each considered stock, over 5000 scenarios. Then we
delete all scenarios where the value of the return of at least one
stock lies outside the interval [
n
of the return of each considered stock, over 5000 scenarios. Then we
delete all scenarios where the value of the return of at least one
stock lies outside the interval [![]() n
-m
n
-m![]() n ,
n , ![]() n
+ m
n
+ m![]() n],
for some value of m. This procedure allows one to reduce the
variability of the scenarios by excluding `extreme'
values of the returns, which can be both positive and negative.
Deletion of a set of scenarios can be performed using the function
spdelscen(). By changing the parameter m, we control the
length of the interval and establish the bounds for possible values
of the returns. The purpose of this procedure is to compare the
solution of the initial problem and the solutions corresponding to
the problems with fewer scenarios having smaller variability.
n],
for some value of m. This procedure allows one to reduce the
variability of the scenarios by excluding `extreme'
values of the returns, which can be both positive and negative.
Deletion of a set of scenarios can be performed using the function
spdelscen(). By changing the parameter m, we control the
length of the interval and establish the bounds for possible values
of the returns. The purpose of this procedure is to compare the
solution of the initial problem and the solutions corresponding to
the problems with fewer scenarios having smaller variability.
As one can intuitively predict, the optimal solution will be `cheaper' if the length of this interval is small, and the contribution rate will increase as the interval length grows, since the minimum return constraint needs to be satisfied for all scenarios, including realizations with extreme unfavorable returns. As a limiting case, when m is large enough to include all the considered set of scenarios, the solution of the original stochastic problem is obtained. These results are summarized in Table 8.

Figure 6.13: Optimal solutions of the stochastic problem for different sets of scenarios.
Figure Optimal solutions of the stochastic problem for different sets of scenarios. shows
the plot of the optimal solution value with respect to the number of
scenarios considered. As one can see, when the number of scenarios
is very close to 5000, the optimal solution is almost the same as
the `true'
solution corresponding to the problem with all 5000 scenarios;
however, as the number of scenarios decreases, the optimal objective
value drops down. This happens because the `extreme'
scenarios that affect the solution are deleted from the scenario
tree, resulting in a less expensive solution. The difference between
the true
solution and the solution obtained after the deletion of scenarios
remains relatively small as long as the number of remaining
scenarios is large enough (![]() 2000). This sufficiently reflects the
variability of the returns; however, this difference rapidly
increases if more scenarios are deleted. In fact, if we leave only
the scenarios where all the returns lie in the interval [
2000). This sufficiently reflects the
variability of the returns; however, this difference rapidly
increases if more scenarios are deleted. In fact, if we leave only
the scenarios where all the returns lie in the interval [![]() n
-
n
-![]() n ,
n , ![]() n
+
n
+ ![]() n],
the optimal solution value is almost twice smaller than in the case
of the full set of 5000 scenarios. These facts show that the
appropriate choice of the scenarios dataset is important for
obtaining the solution of the stochastic problem that would properly
reflect the uncertainty.
n],
the optimal solution value is almost twice smaller than in the case
of the full set of 5000 scenarios. These facts show that the
appropriate choice of the scenarios dataset is important for
obtaining the solution of the stochastic problem that would properly
reflect the uncertainty.
Assemble to order system
Refer to Section 5 in the paper [DVNT05].
Options contract in supply chains
Refer to Section 6 in the paper [DVNT05]
Power management in a hydro-thermal system
Stochastic Programming has been used extensively in the energy sector for various purposes such as planning of capacity expansion, unit commitment, making pricing decision in the electricity market, etc. The following example has been inspired from the work of Gröwe-Kuska et al. (see [GKNR02]). Here we consider a hydro-thermal system in which hourly decisions pertaining to operational levels of the units need to be made under uncertain demand load.
Description
There are T
time periods. I and J are the numbers of thermal and
hydro units, respectively. For a thermal unit i in period t,
ui,t ![]() {0,1}
is its commitment (1 if on, 0 if off) and pi,t its
production, with pi,t = 0 if ui,t =
0, pi,t
{0,1}
is its commitment (1 if on, 0 if off) and pi,t its
production, with pi,t = 0 if ui,t =
0, pi,t ![]() [Pi,tmin, Pi,tmax]
if ui,t = 1. Additionally there are minimum
up/down-time requirements: when unit i is switched on (off)
it must remain on (off) for at least
[Pi,tmin, Pi,tmax]
if ui,t = 1. Additionally there are minimum
up/down-time requirements: when unit i is switched on (off)
it must remain on (off) for at least ![]() iup
(
iup
(![]() idn)
periods. For a hydro plant j, sj,t and wj,t
are its generation and pumping levels in period t with upper
bounds Sj,tmax and Wj,tmax
respectively, and lj,t is the storage volume in
the upper dam at the end of period t with upper bound
Lj,tmax. The water balance relates lj,t
with lj,t-1, sj,t, wj,t
and water inflow
idn)
periods. For a hydro plant j, sj,t and wj,t
are its generation and pumping levels in period t with upper
bounds Sj,tmax and Wj,tmax
respectively, and lj,t is the storage volume in
the upper dam at the end of period t with upper bound
Lj,tmax. The water balance relates lj,t
with lj,t-1, sj,t, wj,t
and water inflow ![]() j,t
using the pumping efficiency
j,t
using the pumping efficiency ![]() j.
The initial and final volumes are specified by ljin
and ljend.
j.
The initial and final volumes are specified by ljin
and ljend.
The basic system requirement is to meet the electric load. Another important requirement is the spinning reserve constraint. To maintain reliability (compensate sudden load peaks or unforeseen outages of units) the total committed capacity should exceed the load in every period by a certain amount (e.g., a fraction of the demand). The load and the spinning reserve during period t are denoted by dt and rt, respectively.
Efficient operation of pumped storage hydro plants exploits daily cycles of load curves by generating during peak load periods and pumping during off-peak periods. Since the operating costs of hydro plants are usually negligible, the total system cost is given by the sum of startup and operating costs of all thermal units over the whole scheduling horizon. The fuel cost Ci,t for operating thermal unit i during period t has the form
Ci,t = max lThe startup cost of unit i depends on its downtime; it may vary from a maximum cold start value to a much smaller value when the unit is still relatively close to its operating temperature. This is modeled by the startup cost
Si,t = maxwhere 0 = ci,0 < ... < ci![]() ic are
fixed cost coefficients.
ic are
fixed cost coefficients. ![]() ic is
the cool-down time of unit i,
ci
ic is
the cool-down time of unit i,
ci![]() ic is
its maximum cold-start cost, ui,
ic is
its maximum cold-start cost, ui,![]()
![]()
![]()
![]() {
{![]() ini,...,0}
are given initial values, where
ini,...,0}
are given initial values, where ![]() ini = maxi
ini = maxi![]() {1,...,I}{
{1,...,I}{![]() ic, 1-
ic, 1-![]() iup,
iup, ![]() idn-1}.
idn-1}.
Model
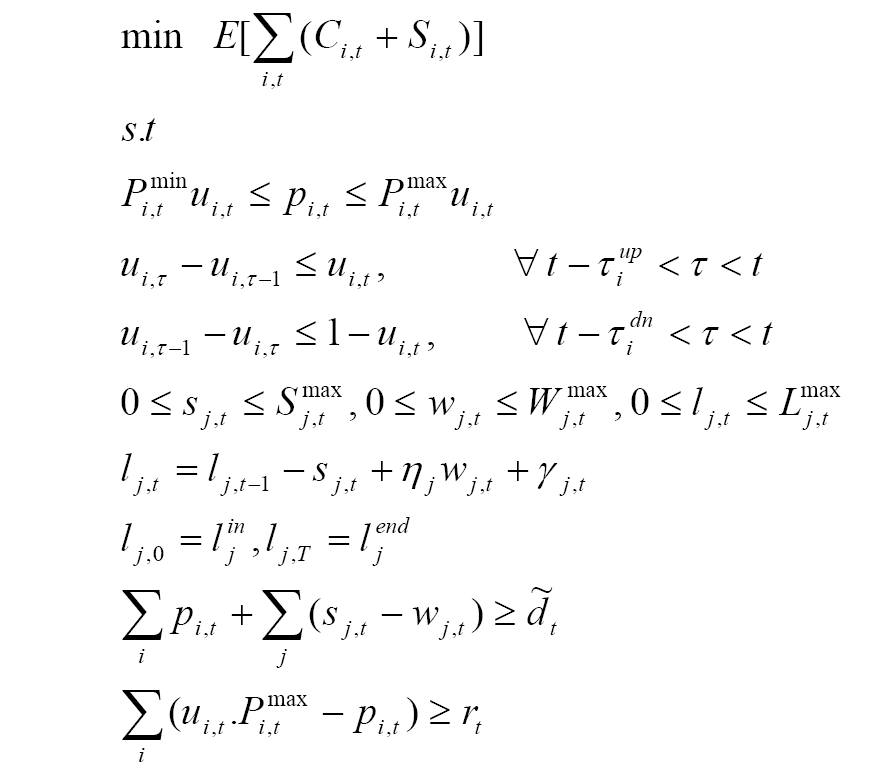
Uncertainty
The uncertainty in the model—demand in each period—is dealt with as follows:
- We begin by aggregation of periods. As the number of periods increases, the possibilities of realization of demand increase exponentially. From the stochastic optimization point of view, some of the consecutive periods may be aggregated together to form a stage, e.g., periods {1,...,t1} may be set to stage 1, periods {t1+1,...,t2} to stage 2,..., and periods {tK+1,...,T} to stage N as shown in the following Figure Aggregated stages.

Figure 6.14: Aggregated stages
- Demand, being
random, may be identified based on a time series or regression
model. Here we simply assume the demand process to be
d˜t =
 t +
t + 
 ˜td˜t-1 +
˜td˜t-1 + 
 ˜t,
where
˜t,
where  ,
,  ,
,  are given, and
are given, and
 ˜t
˜t  Uniform(
Uniform( min,
min, max),
and
max),
and
 ˜t
˜t  Normal(0,1)
Normal(0,1) - Based on the
demand process, we determine an initial structure of the scenario
tree. We compute values of demands in various scenarios using the
sample means and standard deviations of the simulated scenarios by
running M simulations. If
dtm
is the value of demand in the mth run then
estimated
- mean demand:
 t=
t=
, and
Mm m=1t M - variance in demand:
 2t=
2t=

Mm  2
2m=1tt M-1
- mean demand:
- Next, we build a
stable and small scenario tree using the estimates and aggregated
stages as follows:
- Re-model the demand process as
d t=
t=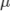
 t+
t+
, where Stg(t) is the aggregated stage where period t belongs to, andt  1/2
1/2t'=2Stg(t')  ˜2, ...,
˜2, ..., ˜N
˜N  {1 w.p 0.5, -1 w.p 0.5}
{1 w.p 0.5, -1 w.p 0.5}
- Generate an
exhaustive binary tree based on possible realizations of
 ˜2, ...,
˜2, ...,  ˜N
as shown below.
˜N
as shown below.
- Re-model the demand process as
Figure 6.15: Binary scenario tree with 2N-1 scenarios
- As the number of
aggregated stages increase, the number of scenarios may increase
rapidly, therefore we may reduce the scenario tree using the
following schema.
- Define the distance between vectors vi and vj
as
ch(vi,vj) = max{1,
 vi
vi h-1,
h-1,  vj
vj h-1}·
h-1}· vi-vj
vi-vj where h is a given parameter, and
where h is a given parameter, and  .
. is a Euclidian
norm.
is a Euclidian
norm.
- Let realizations of
 ˜ = [
˜ = [ ˜2, ...,
˜2, ...,  ˜N] in
scenario k be vector
˜N] in
scenario k be vector  k.
Given S scenarios with probabilities P1,...,PS, we delete a scenario
k = argminl
k.
Given S scenarios with probabilities P1,...,PS, we delete a scenario
k = argminl {1,...,S}{Pl, mins
{1,...,S}{Pl, mins {1,...,S}:s
{1,...,S}:s l ch(
l ch( l,
l, s)}.
Then, roughly speaking, deletion of a scenario k occurs
when it is close to another scenario s as measured by the
distance or where its probability is small. The reduced scenario
tree has one less scenario; scenario k is deleted, and Ps
is incremented by Pk. This step is repeated
until the final number of scenarios reaches a prescribed number S'
that is reasonably small to represent the uncertainty, and would
yield sufficiently accurate solution to the problem.
s)}.
Then, roughly speaking, deletion of a scenario k occurs
when it is close to another scenario s as measured by the
distance or where its probability is small. The reduced scenario
tree has one less scenario; scenario k is deleted, and Ps
is incremented by Pk. This step is repeated
until the final number of scenarios reaches a prescribed number S'
that is reasonably small to represent the uncertainty, and would
yield sufficiently accurate solution to the problem.
- Next, we decouple S' scenarios by:
- Creating a scenario tree with S' branches from the node in the 1st stage, and 1 branch per node from each node in other stages.
- Setting the realized values of
 ˜,
and revised probabilities of scenarios. The scenario tree would
look as shown in the following Figure Reduced scenario tree with S' scenarios.
˜,
and revised probabilities of scenarios. The scenario tree would
look as shown in the following Figure Reduced scenario tree with S' scenarios.
- Many realizations of
 ˜'s
until certain stages are the same, hence we restructure the reduced
scenario tree by clubbing together all the realizations that are
equal as follows:
˜'s
until certain stages are the same, hence we restructure the reduced
scenario tree by clubbing together all the realizations that are
equal as follows:
- Define nodet,n
for the nth node in the tth
stage of the scenario tree. Let PossScent,n be
set of scenarios that branches off from nodet,n
that have same realized values of
 ˜t+1
˜t+1 - Find all such
possible sets of the PossScent,n's
corresponding to the realizations of
 ˜t+1
˜t+1 - Each of the set
PossScent,n forms a new child of nodet,n
with the conditional probability:
 s
s PossScent,nPs / Pt,n,
where Pt,n is the unconditional probability of
occurrence of nodet,n. While keeping track of
number of children of nodet,n, number of nodes
in stage t, and unconditional probability Pt,n
of nodet,n, incrementally build a scenario
tree. The re-structured scenario tree would look as follows.
PossScent,nPs / Pt,n,
where Pt,n is the unconditional probability of
occurrence of nodet,n. While keeping track of
number of children of nodet,n, number of nodes
in stage t, and unconditional probability Pt,n
of nodet,n, incrementally build a scenario
tree. The re-structured scenario tree would look as follows.
- Define nodet,n
for the nth node in the tth
stage of the scenario tree. Let PossScent,n be
set of scenarios that branches off from nodet,n
that have same realized values of
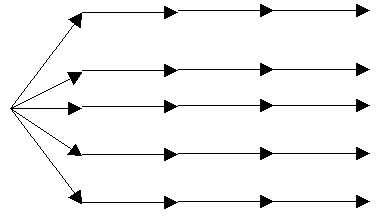
Figure 6.16: Reduced scenario tree with S' scenarios
Figure 6.17: Re-structured scenario tree with S' scenarios
- Define the distance between vectors vi and vj
as
ch(vi,vj) = max{1,
Optimization
The optimization model is built in Xpress-SP by associating all decision variables in period t to Stg(t). The scenario tree is built by running simulation, building a binary scenario tree, and reducing it by deleting few scenarios as described in previous section. The model excerpt is shown below.
declarations
p,S,C: array(ThermalUnits,TimeBlocks) of spvar
u: array(ThermalUnits,(tau_ini..0)+TimeBlocks) of spvar
s,w,l: array(HydroUnits,TimeBlocks) of spvar
lam: array(ThermalUnits,TimeBlocks,1..L) of spvar
TotalCost: splinctr
UBprod: array(ThermalUnits,TimeBlocks) of splinctr
LBprod: array(ThermalUnits,TimeBlocks) of splinctr
UBstoreageBal: array(HydroUnits,TimeBlocks) of splinctr
Minuptime,Mindowntime: dynamic array(ThermalUnits,range,TimeBlocks) of splinctr
Load: array(TimeBlocks) of splinctr
SpinningReserve: array(TimeBlocks) of splinctr
ProdLevel,FuelCost,SumToOne: array(ThermalUnits,TimeBlocks) of splinctr
Prodtn: dynamic array(ThermalUnits,TimeBlocks) of splinctr
StartupCost: array(ThermalUnits,range,TimeBlocks) of splinctr
end-declarations
forall(i in ThermalUnits, t in (tau_ini..0)+TimeBlocks) u(i,t) is_binary
forall(t in tau_ini..0,i in ThermalUnits) do
spsetstage(u(i,t),1)
u(i,t)=0
end-do
forall(i in ThermalUnits,t in TimeBlocks)
UBprod(i,t):=p(i,t)<=P_max(i)*u(i,t)
forall(i in ThermalUnits,t in TimeBlocks)
LBprod(i,t):=p(i,t)>=P_min(i)*u(i,t)
forall(j in HydroUnits,t in TimeBlocks)
s(j,t)<=S_max(j)
forall(j in HydroUnits,t in TimeBlocks)
w(j,t)<=W_max(j)
forall(j in HydroUnits,t in TimeBlocks)
l(j,t)<=SL_max(j)
forall(j in HydroUnits,t in TimeBlocks)
if t=1 then
UBstoreageBal(j,t):= l(j,t)=l_in(j)-s(j,t)+eta(j)*w(j,t)+gamma(j,t)
elif t=T then
UBstoreageBal(j,t):= l_end(j)=l(j,t-1)-s(j,t)+eta(j)*w(j,t)+gamma(j,t)
else
UBstoreageBal(j,t):= l(j,t)=l(j,t-1)-s(j,t)+eta(j)*w(j,t)+gamma(j,t)
end-if
forall(i in ThermalUnits, t in TimeBlocks, tau in (t-tau_up(i)+1)..(t-1) |
t-tau_up(i)+1<=t-1 and tau-1>=tau_ini)
Minuptime(i,tau,t):=u(i,tau)-u(i,tau-1)<=u(i,t)
forall(i in ThermalUnits, t in TimeBlocks, tau in (t-tau_dn(i)+1)..(t-1) |
t-tau_dn(i)+1<=t-1 and tau-1>=tau_ini)
Mindowntime(i,tau,t):=u(i,tau-1)-u(i,tau)<=1-u(i,t)
forall(t in TimeBlocks)
Load(t):=sum(i in ThermalUnits) p(i,t)+
sum(j in HydroUnits) (s(j,t)-w(j,t))>=d(t)
forall(t in TimeBlocks) SpinningReserve(t):=
sum(i in ThermalUnits) (P_max(i)*u(i,t)-p(i,t))>=r(t)
forall(i in ThermalUnits, t in TimeBlocks) do
ProdLevel(i,t):=p(i,t)=
sum(l_ in 1..L) prodt(i,t,l_)*lam(i,t,l_)
FuelCost(i,t):=C(i,t)=sum(l_ in 1..L) cost(i,t,l_)*lam(i,t,l_)
SumToOne(i,t):=sum(l_ in 1..L) lam(i,t,l_)=u(i,t)
Prodtn(i,t):=sum(l_ in 1..L) prodt(i,t,l_)*lam(i,t,l_)
Prodtn(i,t) is_sos2
end-do
forall(i in ThermalUnits,t in TimeBlocks,tau in 0..tau_c(i))
StartupCost(i,tau,t):=
S(i,t)>=c(i,tau)*(u(i,t)-sum(k in 1..tau) u(i,t-k))
TotalCost:=sum(i in ThermalUnits,t in TimeBlocks) (C(i,t)+S(i,t))
Implementation
The model is implemented for 24 time periods (1 day) aggregated into 5 stages, 2 hydro units and 3 thermal units. A visual interface is built to visualize the demand and optimal solutions in various scenarios as shown in the following figure.
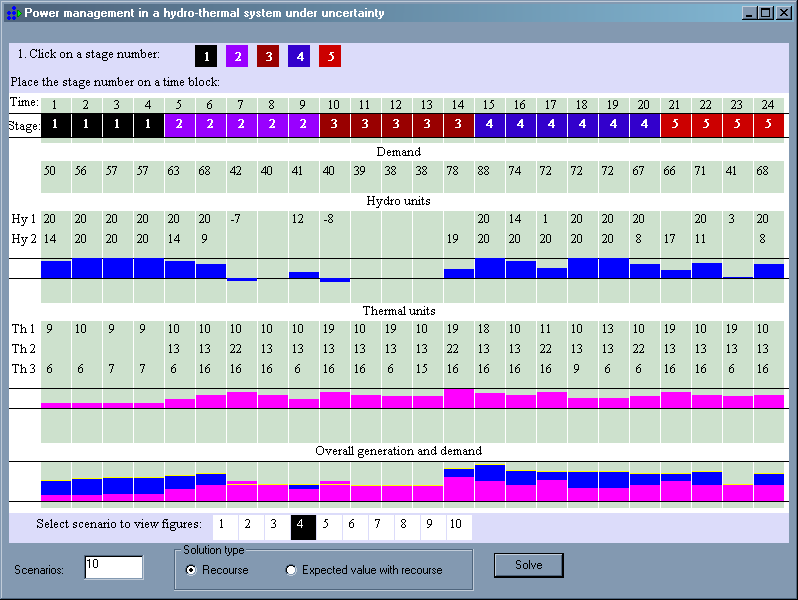
Figure 6.18: Interface for visualization of hydro-thermal generation under uncertain load
If you have any comments or suggestions about these pages, please send mail to docs@dashoptimization.com.