This paper describes several examples of sequential and parallel solving of multiple models with Mosel. Without being able to give an exhaustive list of possible configurations, the examples showcase different uses of the Mosel module mmjobs, such as concurrent execution of several instances of a model, the (sequential) embedding of a submodel into a master, and the implementation of decomposition algorithms (Dantzig-Wolfe and Benders decomposition).
From a more technical point of view, topics discussed in this paper include model management, synchronization of concurrent models, and the use of the shared memory IO driver.
Release 1.6 of Mosel introduces the possibility to work with multiple models directly in the Mosel language. The new functionality, provided by the module mmjobs, includes facilities for model management, synchronization of concurrent models based on event queues, and a shared memory IO driver. The following list gives an overview on the available functionality. For the complete documentation of this module the reader is referred to the section mmjobs of the `Mosel Reference Manual'.
mmjobs introduces two new types, Model and Event.
The type Model is used to reference a Mosel model. Before using the reference to a model it has to be initialized by
loading a bim file.
The type Event represents an event
in the Mosel language.
Events are characterized by a class and a value and
may be exchanged between a model and its parent model.
An event queue is attached to each model to collect all events sent to this
model and is managed with a FIFO policy (First In – First Out).
The first section of this paper introduces the reader to the basic tasks that are typically performed when working with several models in Mosel, namely:
The remainder of the paper gives some more advanced examples of the use of mmjobs with a detailed explanation of their implementation. All examples are available for download from the Dash website.
At this place we would like to stress the difference between multiple models and multiple problems — Mosel works with multiple models but always only a single problem is associated with every model. This means, for instance, if a model contains several calls to a solver such as Xpress-Optimizer, then the solver will work with a single problem representation, and only the solution to the last optimization run can be obtained from the solver at any time.
This section introduces the basic tasks that typically need to be performed when working with several models in Mosel using the functionality of the module mmjobs.
Assume we are given the following simple model testsub.mos (the submodel) that we wish to run from a second model (its master model):
model "Test submodel" forall(i in 10..20) write(i^2, " ") writeln end-model
The reader is certainly familiar with the standard compile-load-run sequence that is always required for the execution of a Mosel model independent of the place from where it is executed (be it the Mosel command line, a host application, or another Mosel model). In the case of a Mosel model executing a second model, we need to augment this standard sequence to compile-load-run-wait. The rationale behind this is that the submodel is started as a separate thread and we thus make sure that the submodel has terminated before the master model ends (or continues its execution with results from the submodel, see Section Communication of data between different models below).
The following model runtestsub.mos uses the compile-load-run-wait sequence in its basic form to execute the model testsub.mos printed above. The corresponding Mosel subroutines are defined by the module mmjobs that needs to be included with a uses statement. The submodel remains as is (that is, there is no need to include mmjobs if the submodel itself does not use any functionality of this module). The last statement of the master model, dropnextevent, may require some further explanation: the termination of the submodel is indicated by an event (of class EVENT_END) that is sent to the master model. The wait statement pauses the execution of the master model until it receives an event. Since in the present case the only event sent by the submodel is this termination message we simply remove the message from the event queue of the master model without checking its nature.
model "Run model testsub"
uses "mmjobs"
declarations
modSub: Model
end-declarations
! Compile the model file
if compile("testsub.mos")<>0 then exit(1); end-if
load(modSub, "testsub.bim") ! Load the bim file
run(modSub) ! Start model execution
wait ! Wait for model termination
dropnextevent ! Ignore termination event message
end-model
The two models are run by executing the master model in any standard way of executing Mosel models (from the Mosel command line, within Xpress-IVE, or from a host application). With the Mosel command line you may use, for instance, the following command:
mosel -c "exec runtestsub.mos"
As a result you should see the following output printed by the submodel (for readers working under Xpress-IVE: please see Section Output from the submodel):
100 121 144 169 196 225 256 289 324 361 400
If we wish to obtain more precise information about the termination status of the submodel we could replace the statement dropnextevent by the following lines that retrieve the event sent by the submodel and print out its class (the termination event has the predefined class EVENT_END) and the value attached to it (here the default value 0). In addition, we display the exit code of the model (value sent by an exit statement terminating the model execution or the default value 0).
declarations
ev: Event
end-declarations
ev:=getnextevent
writeln("Event class: ", getclass(ev))
writeln("Event value: ", getvalue(ev))
writeln("Exit code : ", getexitcode(modSub))
If a submodel execution takes a long time it may be desirable to interrupt the submodel without stopping the master model itself. The following modified version of our master model (file runsubwait.mos) shows how this can be achieved by adding a duration (in seconds) to the wait statement. If the submodel has not yet sent the termination event message after executing for one second it is stopped by the call to stop with the model reference.
model "Run model testsub"
uses "mmjobs"
declarations
modSub: Model
end-declarations
! Compile the model file
if compile("testsub.mos")<>0 then exit(1); end-if
load(modSub, "testsub.bim") ! Load the bim file
run(modSub) ! Start model execution
wait(1) ! Wait 1 second for an event
if isqueueempty then ! No event has been sent: model still runs
writeln("Stopping the submodel")
stop(modSub) ! Stop the model
wait ! Wait for model termination
end-if
dropnextevent ! Ignore termination event message
end-model
Readers who have tried to execute the master models from the previous sections within Xpress-IVE will not have seen any output from the submodel since IVE only captures the output from the master model. The best way to obtain access to the submodel output in this case is to redirect this output to a file. Redirecting the submodel output may also become necessary when several (sub)models are run in parallel as the output on screen is likely to mix up output printed by several of these models.
Output may be redirected directly within the submodel with statements like the following added to the model before any output is printed:
fopen("testout.txt", F_OUTPUT+F_APPEND) ! Output to file (in append mode)
fopen("tee:testout.txt&", F_OUTPUT) ! Output to file and on screen
fopen("null:", F_OUTPUT) ! Disable all output
where the first line redirects the output to the file testout.txt, the second statement maintains the output on screen while writing to the file at the same time, and the third line makes the model entirely silent. The output file is closed by adding the statement fclose(F_OUTPUT) after the printing statements in the model.
The same can be achieved from the master model by adding output redirection before the run statement for the corresponding submodel, such as:
setdefstream(modSub, F_OUTPUT, "testout.txt") ! Output to file
setdefstream(modSub, F_OUTPUT, "tee:testout.txt&")
! Output to file and on screen
setdefstream(modSub, F_OUTPUT, "null:") ! Disable all output
The output redirection for a submodel may be terminated by resetting its output stream to the default output:
setdefstream(modSub, F_OUTPUT, "")
The default compilation of a Mosel file filename.mos generates a binary model file filename.bim. To avoid the generation of physical BIM files for submodels we may compile the submodel to memory, as shown in the following example runsubmem.mos. Working in memory usually is more efficient than accessing physical files. Furthermore, this feature will also be helpful if you do not have write access at the place where the master model is executed.
model "Run model testsub"
uses "mmjobs", "mmsystem"
declarations
modSub: Model
end-declarations
! Compile the model file
if compile("", "testsub.mos", "shmem:testsubbim")<>0 then
exit(1)
end-if
load(modSub, "shmem:testsubbim") ! Load the bim file from memory
fdelete("shmem:testsubbim") ! ... and release the memory block
run(modSub) ! Start model execution
wait ! Wait for model termination
dropnextevent ! Ignore termination event message
end-model
The full version of compile takes three arguments: the compilation flags (e.g., use "g" for debugging), the model file name, and the output file name (here a label prefixed by the name of the shared memory driver). Having loaded the model we may free the memory used by the compiled model with a call to fdelete (this subroutine is provided by the module mmsystem that needs to be loaded in addition to mmjobs).
A convenient means of modifying data in a Mosel model when running the model (that is, without having to modify the model itself and recompile it) is to use runtime parameters. Such parameters are declared at the beginning of the model in a parameters block where every parameter is given a default value that will be applied if no other value is specified for this parameter at the model execution.
Consider the following model rtparams.mos that may receive parameters of four different types—integer, real, string, and Boolean—and prints out their values.
model "Runtime parameters" parameters PARAM1 = 0 PARAM2 = 0.5 PARAM3 = '' PARAM4 = false end-parameters writeln(PARAM1, " ", PARAM2, " ", PARAM3, " ", PARAM4) end-model
The master model runrtparam.mos executing this (sub)model may look as follows—all runtime parameters are given new values:
model "Run model rtparams"
uses "mmjobs"
declarations
modPar: Model
end-declarations
! Compile the model file
if compile("rtparams.mos")<>0 then exit(1); end-if
load(modPar, "rtparams.bim") ! Load the bim file
! Start model execution
run(modPar, "PARAM1=" + 2 + ",PARAM2=" + 3.4 +
",PARAM3='a string'" + ",PARAM4=" + true)
wait ! Wait for model termination
dropnextevent ! Ignore termination event message
end-model
Once we have seen how to run a parameterized model from a master model it is only a small step to the execution of several different submodel instances from a master model. The two following sections deal with the two cases of sequential and parallel execution of submodels. For simplicity's sake, the submodels in our examples are all parameterized versions of a single model. It is of course equally possible to compile, load, and run different submodel files from a single master model.
Running several instances of a submodel in sequence only requires small modifications to the master model that we have used for a single model instance as can be seen from the following example (file runrtparamseq.mos)—to keep things simple, we now only reset a single parameter at every execution:
model "Run model rtparams in sequence"
uses "mmjobs"
declarations
A = 1..10
modPar: Model
end-declarations
! Compile the model file
if compile("rtparams.mos")<>0 then exit(1); end-if
load(modPar, "rtparams.bim") ! Load the bim file
forall(i in A) do
run(modPar, "PARAM1=" + i) ! Start model execution
wait ! Wait for model termination
dropnextevent ! Ignore termination event message
end-do
end-model
The submodel is compiled and loaded once and after starting the execution of a submodel instance we wait for its termination before the next instance is started.
The parallel execution of submodel (instances) requires slightly more modifications. We still have to compile the submodel only once, but it now needs to be loaded as many times as we want to run parallel instances. The wait statements are now moved to a separate loop since we first want to start all submodels and then wait for their termination.
model "Run model rtparams in parallel"
uses "mmjobs"
declarations
A = 1..10
modPar: array(A) of Model
end-declarations
! Compile the model file
if compile("rtparams.mos")<>0 then exit(1); end-if
forall(i in A) do
load(modPar(i), "rtparams.bim") ! Load the bim file
run(modPar(i), "PARAM1=" + i) ! Start model execution
end-do
forall(i in A) do
wait ! Wait for model termination
dropnextevent ! Ignore termination event message
end-do
end-model
The order in which the submodel output appears on screen is nondeterministic because the models are run in parallel. However, since the submodel execution is very quick, this may not become obvious: try adding the line wait(1) to the submodel rtparams.mos immediately before the writeln statement (you will also need to add the statement uses "mmjobs" at the beginning of the model) and compare the output of several runs of the master model. You are now likely to see different output sequences with every run.
Runtime parameters are a means of communicating single data values to a submodel but they are not suited, for instance, to pass data tables or sets to a submodel. Also, they cannot be employed to retrieve any information from a submodel or to exchange data between models during their execution. All these tasks are addressed by the two IO drivers defined by the module mmjobs: the shmem driver and the mempipe driver. As was already stated earlier, the shmem driver is meant for one-to-many communication (one model writing, many reading) and the mempipe driver serves for many-to-one communication. In the case of one model writing and one model reading we may use either, where shmem is conceptionally probably the easier to use.
With the shmem shared memory driver we write and read data blocks from/to memory. The use of this driver is quite similar to the way we would work with physical files. We have already encountered an example of its use in Section Compilation to memory: the filename is replaced by a label, prefixed by the name of the driver, such as "mmjobs.shmem:aLabel". If the module mmjobs is loaded by the model (or another model held in memory at the same time, such as its master model) we may use the short form "shmem:aLabel".
The exchange of data between different models is carried out through initializations blocks. In general, the shmem driver will be combined with the raw driver to save data in binary format.
Let us now take a look at a modified version testsubshm.mos of our initial test submodel (Section Executing a submodel). This model reads in the index range from memory and writes back the resulting array to memory:
model "Test submodel" declarations A: range B: array(A) of real end-declarations initializations from "raw:" A as "shmem:A" end-initializations forall(i in A) B(i):= i^2 initializations to "raw:" B as "shmem:B" end-initializations end-model
The master model runsubshm.mos to run this submodel may look as follows:
model "Run model testsubshm"
uses "mmjobs"
declarations
modSub: Model
A = 30..40
B: array(A) of real
end-declarations
! Compile the model file
if compile("testsubshm.mos")<>0 then exit(1); end-if
load(modSub, "testsubshm.bim") ! Load the bim file
initializations to "raw:"
A as "shmem:A"
end-initializations
run(modSub) ! Start model execution
wait ! Wait for model termination
dropnextevent ! Ignore termination event message
initializations from "raw:"
B as "shmem:B"
end-initializations
writeln(B)
end-model
Before the submodel run is started the index range is written to memory and after its end we retrieve the result array to print it out from the master model.
If memory blocks are no longer used it is recommended to free up these blocks by calling fdelete (subroutine provided by module mmsystem), especially if the data blocks are large, since the data blocks survive the termination of the model that has created them, even if the model is unloaded explicitly, until the module mmjobs is unloaded (explicitly or by the termination of the Mosel session). At the end of our master model we might thus add the lines
fdelete("shmem:A")
fdelete("shmem:B")
The memory pipe IO driver mempipe works in the opposite way to what we have seen for the shared memory driver: a pipe first needs to be opened before it can be written to. That means we need to call initializations from before initializations to. The submodel (file testsubpip.mos) now looks as follows:
model "Test submodel" declarations A: range B: array(A) of real end-declarations initializations from "mempipe:indata" A end-initializations forall(i in A) B(i):= i^2 initializations to "mempipe:resdata" B end-initializations end-model
This is indeed not very different from the previous submodel. However, there are more changes to the master model (file runsubpip.mos): the input data is now written by the master model after the submodel run has started. The master model then opens a new pipe to read the result data before the submodel terminates its execution.
model "Run model testsubpip"
uses "mmjobs"
declarations
modSub: Model
A = 30..40
B: array(A) of real
end-declarations
! Compile the model file
if compile("testsubpip.mos")<>0 then exit(1); end-if
load(modSub, "testsubpip.bim") ! Load the bim file
run(modSub) ! Start model execution
initializations to "mempipe:indata"
A
end-initializations
initializations from "mempipe:resdata"
B
end-initializations
wait ! Wait for model termination
dropnextevent ! Ignore termination event message
writeln(B)
end-model
Once a file has opened a pipe for reading it remains blocked in this state until it has received the requested data through this pipe. The program control flow is therefore the following in the present case:
The cutting stock example we are working with in this section is taken from the `Mosel User Guide'. The reader is refered to this manual for further detail on the column generation algorithm and its implementation with Mosel.
Column generation algorithms are typically used for solving linear problems with a huge number of variables for which it is not possible to generate explicitly all columns of the problem matrix. Starting with a very restricted set of columns, after each solution of the problem a column generation algorithm adds one or several columns that improve the current solution.
Our column generation algorithm for the cutting stock problem requires us to solve a knapsack problem based on the dual value of the current solution to determine a new column (= cutting pattern). The difference between the User Guide implementation and the one shown below consists in the handling of this knapsack (sub)problem. In the User Guide implementation Mosel's constraint hiding functionality is used to blend out subsets of constraints; in the version shown below the subproblem is implemented in a model on its own. Both versions implement exactly the same algorithm and their performance is comparable. On larger instances, however, the two-model version is likely to be slightly more efficient, since every model defines exactly the problem to be solved, without any selection of (un)hidden constraints.
In this example, the changes to the problems are such that they cause complete re-loading of the problems for every optimization run. A clearer advantage of the multi-model version would show up if there were only slight changes (bound updates) to the main (cutting stock) problem so that this problem did not have to be reloaded into the solver for every new run.
A paper mill produces rolls of paper of a fixed width MAXWIDTH that are subsequently cut into smaller rolls according to the customer orders. The rolls can be cut into NWIDTHS different sizes. The orders are given as demands for each width i (DEMANDi). The objective of the paper mill is to satisfy the demand with the smallest possible number of paper rolls in order to minimize the losses.
The objective of minimizing the total number of rolls can be expressed as choosing the best set of cutting patterns for the current set of demands. Since it may not be obvious how to calculate all possible cutting patterns by hand, we start off with a basic set of patterns (PATTERNS_1,..., PATTERNSNWIDTH), that consists of cutting small rolls all of the same width as many times as possible out of the large roll.
If we define variables usej to denote the number of times a cutting pattern j (j ![]() WIDTHS = {1,...,NWIDTH}) is used, then
the objective becomes to minimize the sum of these variables, subject to the constraints that the demand for every size has
to be met.
WIDTHS = {1,...,NWIDTH}) is used, then
the objective becomes to minimize the sum of these variables, subject to the constraints that the demand for every size has
to be met.
| j |
| j |
The paper mill can satisfy the demand with just the basic set of cutting patterns, but it is likely to incur significant losses through wasting more than necessary of every large roll and by cutting more small rolls than its customers have ordered. We therefore employ a column generation heuristic to find more suitable cutting patterns.
Our heuristic performs a column generation loop at the top node, before starting the MIP search. Every iteration of the column generation loop executes the following steps:
Step 3 of this loop requires us to solve an integer knapsack problem of the form
| j |
| j |
This second optimization problem is independent of the main, cutting stock problem since the two have no variables in common.
The implementation is divided into two parts: the master model (file paperp.mos) with the definition of the cutting stock problem and the column generation algorithm, and the knapsack model (file knapsack.mos) that is run from the master.
The main part of the cutting stock model looks as follows:
model "Papermill (multi-prob)"
uses "mmxprs", "mmjobs"
forward procedure column_gen
forward function knapsack(C:array(range) of real,
A:array(range) of real,
B:real,
xbest:array(range) of integer): real
declarations
NWIDTHS = 5 ! Number of different widths
WIDTHS = 1..NWIDTHS ! Range of widths
RP: range ! Range of cutting patterns
MAXWIDTH = 94 ! Maximum roll width
EPS = 1e-6 ! Zero tolerance
WIDTH: array(WIDTHS) of real ! Possible widths
DEMAND: array(WIDTHS) of integer ! Demand per width
PATTERNS: array(WIDTHS, WIDTHS) of integer ! (Basic) cutting patterns
use: array(RP) of mpvar ! Rolls per pattern
soluse: array(RP) of real ! Solution values for variables `use'
Dem: array(WIDTHS) of linctr ! Demand constraints
MinRolls: linctr ! Objective function
Knapsack: Model ! Reference to the knapsack model
end-declarations
WIDTH:: [ 17, 21, 22.5, 24, 29.5]
DEMAND:: [150, 96, 48, 108, 227]
! Make basic patterns
forall(j in WIDTHS) PATTERNS(j,j) := floor(MAXWIDTH/WIDTH(j))
forall(j in WIDTHS) do
create(use(j)) ! Create NWIDTHS variables `use'
use(j) is_integer ! Variables are integer and bounded
use(j) <= integer(ceil(DEMAND(j)/PATTERNS(j,j)))
end-do
MinRolls:= sum(j in WIDTHS) use(j) ! Objective: minimize no. of rolls
! Satisfy all demands
forall(i in WIDTHS)
Dem(i):= sum(j in WIDTHS) PATTERNS(i,j) * use(j) >= DEMAND(i)
res:= compile("knapsack.mos") ! Compile the knapsack model
load(Knapsack, "knapsack.bim") ! Load the knapsack model
column_gen ! Column generation at top node
minimize(MinRolls) ! Compute the best integer solution
! for the current problem (including
! the new columns)
writeln("Best integer solution: ", getobjval, " rolls")
write(" Rolls per pattern: ")
forall(i in RP) write(getsol(use(i)),", ")
writeln
end-model
Before starting the column generation heuristic (the definition of procedure column_gen is left out here since it remains unchanged from the User Guide example) the knapsack model is compiled and loaded so that at every column generation loop we merely need to run it with new data. The knapsack model is run from the function knapsack that takes as its parameters the data for the knapsack problem and its solution values. The function saves all data to shared memory, then runs the knapsack model and retrieves the solution from shared memory. Its return value is the objective value (zbest) of the knapsack problem.
function knapsack(C:array(range) of real,
A:array(range) of real,
B:real,
xbest:array(range) of integer):real
initializations to "raw:noindex"
A as "shmem:A" B as "shmem:B" C as "shmem:C"
end-initializations
run(Knapsack, "NWIDTHS="+NWIDTHS) ! Start solving knapsack subproblem
wait ! Wait until subproblem finishes
dropnextevent ! Ignore termination message
initializations from "raw:"
xbest as "shmem:xbest" returned as "shmem:zbest"
end-initializations
end-function
To enforce a sequential execution of the two models (we need to retrieve the results from the knapsack problem before we may continue with the master) we must add a call to the procedure wait immediately after the run statement. Otherwise the execution of the master model continues concurrently to the child model. On termination, the child model sends a `termination' event (an event of class EVENT_END). Since our algorithm does not require this event we simply remove it from the model's event queue with a call to dropnextevent.
The implementation of the knapsack model is straightforward. All problem data is obtained from shared memory and after solving the problem its solution is saved into shared memory.
model "Knapsack" uses "mmxprs" parameters NWIDTHS=5 ! Number of different widths end-parameters declarations WIDTHS = 1..NWIDTHS ! Range of widths A,C: array(WIDTHS) of real ! Constraint + obj. coefficients B: real ! RHS value of knapsack constraint KnapCtr, KnapObj: linctr ! Knapsack constraint+objective x: array(WIDTHS) of mpvar ! Knapsack variables xbest: array(WIDTHS) of integer ! Solution values end-declarations initializations from "raw:noindex" A as "mmjobs.shmem:A" B as "mmjobs.shmem:B" C as "mmjobs.shmem:C" end-initializations ! Define the knapsack problem KnapCtr:= sum(j in WIDTHS) A(j)*x(j) <= B KnapObj:= sum(j in WIDTHS) C(j)*x(j) forall(j in WIDTHS) x(j) is_integer ! Solve the problem and retrieve the solution maximize(KnapObj) z:=getobjval forall(j in WIDTHS) xbest(j):=round(getsol(x(j))) initializations to "raw:" xbest as "mmjobs.shmem:xbest" z as "mmjobs.shmem:zbest" end-initializations end-model
In this model we have prefixed the shared memory driver shmem with the name of the module mmjobs. Doing so is only required if we want to be able to run the knapsack model separately, that is, without the cutting stock master model that loads the mmjobs module into memory.
Another case where we would have to explicitly add the name of a module to a driver occurs when we need to distinguish between several shmem drivers defined by different modules.
With the data in the model above, the column generation algorithm generates 6 new patterns, taking the value of the LP-relaxation of the cutting stock problem from originally 177.67 down to 160.95. The MIP finds a solution with 161 rolls using the following patterns:
| Widths | ||||||
|---|---|---|---|---|---|---|
| Pattern | 17 | 21 | 22.5 | 24 | 29.5 | Usage |
| 3 | 0 | 0 | 4 | 0 | 0 | 1 |
| 5 | 0 | 0 | 0 | 0 | 3 | 15 |
| 6 | 0 | 1 | 0 | 3 | 0 | 32 |
| 8 | 2 | 0 | 0 | 0 | 2 | 75 |
| 10 | 0 | 2 | 1 | 0 | 1 | 32 |
| 11 | 0 | 0 | 2 | 2 | 0 | 6 |
In this section we show how to execute several models in parallel and communicate solution information among these models. This scheme may be particularly interesting when working with Mosel on a multi-processor machine, e.g. by starting a number of models that corresponds to the available number of processors.
Our idea is to run several instances (different only by the parameterization of the solution algorithm) of the same MIP model concurrently and to stop the entire run when the first model has finished. If the different solution algorithms are complementary in the sense that some quickly produce (good) solutions and others are better at proving optimality once the best solution is found then one may reasonably expect an additional synergy effect from exchanging solution updates during the MIP search.
To implement this scheme, we define a master model that starts the model runs and coordinates the solution updates, and a parameterizable child model that is loaded and run with the desired number of versions. The child models all use the same solver (Xpress-Optimizer) but it would equally be possible to use a different solver for some of the child models, provided it defines the necessary functionality for interacting with the search.
Economic lot sizing (ELS) considers production planning over a given planning horizon, in our example a range of time periods TIMES = 1,...,T. In every period t, there is a given demand DEMANDpt for every product p (p ![]() PRODUCTS) that must be satisfied by the
production in this period and by inventory carried over from previous periods.
PRODUCTS) that must be satisfied by the
production in this period and by inventory carried over from previous periods.
A set-up cost SETUPCOSTt is associated with production in a period, and the total production capacity per period, CAPt, is limited. The unit production cost PRODCOSTpt per product and time period is also given. There is no inventory or stock-holding cost.
We introduce the decision variables producept for the amount of product p made in period t and the binary variables setuppt indicating whether a setup takes place for product p in period t (setuppt = 1) or not (setuppt = 0).
We may then formulate the following mathematical model for this problem:
| t |
| p |
| p |
| t |
| s = 1 |
| t |
| s = 1 |
| p |
The objective function is to minimize the total cost. The constraints in the second line formulate the requirement that the production of p in periods 0 to t must satisfy the total demand for this product during this period of time. The next set of constraints establish the implication `if there is production during t then there is a setup in t' where Dptl stands for the demand of product p in periods t to l. The production capacity per period t is limited. And finally, the setuppt variables are binaries.
A well-known class of valid inequalities for ELS are the so-called (l,S)-inequalities [PW94]. If Dptl denotes the total demand of p in periods t to l, then for each period l and each subset of periods S of 1 to l, the (l,S)-inequality is
| l |
| t = 1 | t |
| l |
| t = 1 | t |
It says that actual production producept in the periods included in S plus the maximum potential production Dptl · setuppt in the remaining periods (those not in S) must at least equal the total demand in periods 1 to l.
It is possible to develop the following cutting plane algorithm based on these (l,S)-inequalities:
| l |
| t = 1 |
There are numerous options for how to configure this algorithm. For instance:
The implementation of the (l,S)-cut generation algorithm shown below may be configured to generate cuts at the top node only (TOPONLY = true) and to generate one or several rounds of cuts (SEVERALROUNDS = true).
With mmjobs events are always sent between parent – child pairs, not directly from one child to another. The 'solution found' message therefore needs to be sent to the parent model that then passes on this message to all other child models.
Another point that should be stressed is the fact that we only compile the ELS model file once, but the number of instances loaded into memory needs to correspond to the number of child models we wish to run.
The master model compiles, loads and runs the child models and coordinates the solution updates. Some care must be taken with the solution updates since new solutions that are reported are not guaranteed to be better than others previously reported by other child models. For instance, if two models find solutions almost at the same time, the first solution that reaches the master may be the better one and it must not be overridden by the next.
For a nice solution display at the end, the master model also reads in parts of the problem data from file.
model "Els master"
uses "mmjobs"
parameters
DATAFILE = "els5.dat"
T = 45
P = 4
end-parameters
declarations
RM = 0..5 ! Range of models
TIMES = 1..T ! Time periods
PRODUCTS = 1..P ! Set of products
solprod: array(PRODUCTS,TIMES) of real ! Sol. values for var.s produce
solsetup: array(TIMES) of real ! Sol. values for var.s setup
DEMAND: array(PRODUCTS,TIMES) of integer ! Demand per period
modELS: array(RM) of Model ! Models
modid: array(set of integer) of integer ! Model indices
NEWSOL = 2 ! Identifier for "sol. found" event
Msg: Event ! Messages sent by models
end-declarations
! Compile, load, and run models M1 and M2
M1:= 1; M2:=2
res:= compile("elsp.mos")
load(modELS(M1), "elsp.bim")
load(modELS(M2), "elsp.bim")
forall(m in RM) modid(getid(modELS(m))):= m
run(modELS(M1), "ALG="+M1+",DATAFILE="+DATAFILE+",T="+T+",P="+P)
run(modELS(M2), "ALG="+M2+",DATAFILE="+DATAFILE+",T="+T+",P="+P)
objval:= MAX_REAL
algsol:= -1; algopt:= -1
repeat
wait ! Wait for the next event
Msg:= getnextevent ! Get the event
if getclass(Msg)=NEWSOL then ! Get the event class
if getvalue(Msg) < objval then ! Value of the event (= obj. value)
algsol:= modid(getfromid(Msg)) ! ID of model sending the event
objval:= getvalue(Msg)
writeln("Improved solution ", objval, " found by model ", algsol)
forall(m in RM | m <> algsol) send(modELS(m), NEWSOL, objval)
else
writeln("Solution ", getvalue(Msg), " found by model ",
modid(getfromid(Msg)))
end-if
end-if
until getclass(Msg)=EVENT_END ! A model has finished
algopt:= modid(getfromid(Msg)) ! Retrieve ID of terminated model
forall(m in RM) stop(modELS(m)) ! Stop all running models
! Retrieve the best solution from shared memory
initializations from "raw:noindex"
solprod as "shmem:solprod"+algsol
solsetup as "shmem:solsetup"+algsol
end-initializations
initializations from DATAFILE
DEMAND
end-initializations
! Solution printing
writeln("Best solution found by model ", algsol)
writeln("Optimality proven by model ", algopt)
writeln("Objective value: ", objval)
write("Period setup ")
forall(p in PRODUCTS) write(strfmt(p,-7))
forall(t in TIMES) do
write("\n ", strfmt(t,2), strfmt(solsetup(t),8), " ")
forall(p in PRODUCTS) write(strfmt(solprod(p,t),3), " (",DEMAND(p,t),")")
end-do
writeln
end-model
In this implementation we define an array modid that establishes the correspondence between the model index used in our model and Mosel's internal ID of the model. Whenever a child model sends an event to the master, we retrieve its ID (with function getfromid) and store the corresponding model index, to be able to use it for solution printing later on.
The ELS child model is written in such a way that the model can be executed separately. In particular, every model performs the complete initialization of its data from file, a task that for greater efficiency could be reserved to the master model, communicating data via shared memory to the child models (however, in our example data handling time is negligible compared to the running time of the solution algorithms).
The main part of the ELS model contains the definition of the model itself and the selection of the solution algorithm:
model Els
uses "mmxprs","mmjobs"
parameters
ALG = 0 ! Default algorithm: no user cuts
DATAFILE = "els4.dat"
T = 60
P = 4
end-parameters
forward procedure tree_cut_gen
forward public function cb_node: boolean
forward public function cb_updatebnd(node:integer): integer
forward public procedure cb_intsol
declarations
NEWSOL = 2 ! "New solution" event class
EPS = 1e-6 ! Zero tolerance
TIMES = 1..T ! Time periods
PRODUCTS = 1..P ! Set of products
DEMAND: array(PRODUCTS,TIMES) of integer ! Demand per period
SETUPCOST: array(TIMES) of integer ! Setup cost per period
PRODCOST: array(PRODUCTS,TIMES) of real ! Production cost per period
CAP: array(TIMES) of integer ! Production capacity per period
D: array(PRODUCTS,TIMES,TIMES) of integer ! Total demand in periods t1 - t2
produce: array(PRODUCTS,TIMES) of mpvar ! Production in period t
setup: array(TIMES) of mpvar ! Setup in period t
solprod: array(PRODUCTS,TIMES) of real ! Sol. values for var.s produce
solsetup: array(TIMES) of real ! Sol. values for var.s setup
Msg: Event ! An event
end-declarations
initializations from DATAFILE
DEMAND SETUPCOST PRODCOST CAP
end-initializations
forall(p in PRODUCTS,s,t in TIMES) D(p,s,t):= sum(k in s..t) DEMAND(p,k)
! Objective: minimize total cost
MinCost:= sum(t in TIMES) (SETUPCOST(t) * setup(t) +
sum(p in PRODUCTS) PRODCOST(p,t) * produce(p,t) )
! Production in period t must not exceed the total demand for the
! remaining periods; if there is production during t then there
! is a setup in t
forall(t in TIMES)
sum(p in PRODUCTS) produce(p,t) <= sum(p in PRODUCTS) D(p,t,T) * setup(t)
! Production in periods 0 to t must satisfy the total demand
! during this period of time
forall(p in PRODUCTS,t in TIMES)
sum(s in 1..t) produce(p,s) >= sum (s in 1..t) DEMAND(p,s)
! Capacity limits
forall(t in TIMES) sum(p in PRODUCTS) produce(p,t) <= CAP(t)
forall(t in TIMES) setup(t) is_binary ! Variables setup are 0/1
setparam("zerotol", EPS/100) ! Set Mosel comparison tolerance
SEVERALROUNDS:=false; TOPONLY:=false
case ALG of
1: do
setparam("XPRS_CUTSTRATEGY", 0) ! No cuts
setparam("XPRS_HEURSTRATEGY", 0) ! No heuristics
end-do
2: do
setparam("XPRS_CUTSTRATEGY", 0) ! No cuts
setparam("XPRS_HEURSTRATEGY", 0) ! No heuristics
setparam("XPRS_PRESOLVE", 0) ! No presolve
end-do
3: tree_cut_gen ! User branch&cut (single round)
4: do ! User branch&cut (several rounds)
tree_cut_gen
SEVERALROUNDS:=true
end-do
5: do ! User cut&branch (several rounds)
tree_cut_gen
SEVERALROUNDS:=true
TOPONLY:=true
end-do
end-case
! Parallel setup
setcallback(XPRS_CB_PRENODE, "cb_updatebnd") ! Node pre-treatment callback
setcallback(XPRS_CB_INTSOL, "cb_intsol") ! Integer solution callback
setparam("XPRS_SOLUTIONFILE",0) ! Do not save solutions to file
! Solve the problem
minimize(MinCost)
end-model
The procedure tree_cut_gen sets up a user cut generation routine, configurable to generate cuts only at the top node of the branch-and-bound search (TOPONLY) or to execute one or several cut generation iterations per node (SEVERALROUNDS). The definition of the cut generation routine cb_node itself is left out here.
procedure tree_cut_gen
setparam("XPRS_HEURSTRATEGY", 0) ! Switch heuristics off
setparam("XPRS_CUTSTRATEGY", 0) ! Switch automatic cuts off
setparam("XPRS_PRESOLVE", 0) ! Switch presolve off
setparam("XPRS_EXTRAROWS", 5000) ! Reserve extra rows in matrix
setcallback(XPRS_CB_CUTMGR, "cb_node") ! Define the cut manager callback
end-procedure
The communication between concurrently running child models has two parts: (a) any integer solution found must be saved and comunicated to the master model and (b) bound updates sent by the master problem must be incorporated into the search. Xpress-Optimizer provides a specific integer solution callback for saving solutions into user structures. An obvious place for bound updates in nodes is the cut-manager callback function. However, this function being already in use for other purposes with certain settings of the algorithm, we employ a different callback function that also gets called at every node, the node pre-treatment callback.
! Update cutoff value
public function cb_updatebnd(node:integer): integer
if not isqueueempty then
repeat
Msg:= getnextevent
until isqueueempty
newcutoff:= getvalue(Msg)
setparam("XPRS_MIPABSCUTOFF", newcutoff)
if (newcutoff < getparam("XPRS_LPOBJVAL")) then
returned:= 1 ! Node becomes infeasible
end-if
end-if
end-function
! Store and communicate new solution
public procedure cb_intsol
objval:= getparam("XPRS_LPOBJVAL") ! Retrieve current objective value
cutoff:= getparam("XPRS_MIPABSCUTOFF")
if(cutoff > objval) then
setparam("XPRS_MIPABSCUTOFF", objval)
end-if
! Get the solution values
forall(t in TIMES) do
forall(p in PRODUCTS) solprod(p,t):=getsol(produce(p,t))
solsetup(t):=getsol(setup(t))
end-do
! Store the solution in shared memory
initializations to "raw:noindex"
solprod as "shmem:solprod"+ALG
solsetup as "shmem:solsetup"+ALG
end-initializations
! Send "solution found" signal
send(NEWSOL, objval)
end-procedure
The bound update callback function checks whether the event queue contains any events, if this is the case, it takes all events from the queue and sets the value of the last event as the new cutoff value. The rationale behind the loop for emptying the event queue is that the master model may have sent several improved solution values since the last check, the best value is always the one sent last, that is, the last in the queue.
The integer solution callback writes the solution values to shared memory, adding the identifier of the model (= value of ALG). The latter ensures that two child models that possibly write out their solution at the same time do not use the same memory area.
A run with two models may generate a log similar to the following one (note that the model that terminates the search is not the same that has found the optimal solution).
Improved solution 1283 found by model 2 Improved solution 1250 found by model 2 Improved solution 1242 found by model 1 Improved solution 1236 found by model 2 Improved solution 1234 found by model 2 Best solution found by model 2 Optimality proven by model 1 Objective value: 1234
Dantzig-Wolfe decomposition (see [Teb01] for further detail) is a solution method for problems where, if a relatively small number of constraints were removed, the problem would fall apart into a number of independent problems. This means, it is possible to re-order the rows and columns of the constraint matrix as shown in Figure Coeffcient matrix with primal block angular structure, where non-zero coefficients only occur within the gray shaded areas. Such a primal block angular structure may become immediately apparent by visualizing a problem matrix with Xpress-IVE. However, in most cases it will be necessary to re-organize the constraint definitions, grouping them by common index (sub)sets such as time periods, products, plant locations, and so on.
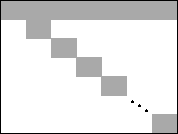
Figure 1: Coeffcient matrix with primal block angular structure
The constraints (including the objective function) involving variables of several or all subproblems are referred to as global constraints (also: common, linking, or master constraints). These constraints are used to form the master problem. The individual blocks on the diagonal of the coefficient matrix are solved as pricing subproblems, coordinated by the master problem. By solving the master problem we obtain a solution to the original problem. Since the master problem has a large number of variables (defined by the set of basic feasible solutions and unbounded directions of the pricing problems), we work with a restricted master problem over a small subset of the variables. The variables to enter the active set of variables of the restricted master problem are determined by solving the pricing subproblems. With objective functions for the pricing problems that are based on the dual values of the restricted master problem we can obtain that the objective function value at each extreme point is the reduced cost (or price) of the master problem variable associated with the extreme point.
For maximization problems, solving the modified pricing problems generates basic feasible solutions of maximum reduced cost. If the objective value at an extreme point is positive, then the associated master problem variable is added to the master problem; if the minimum objective value over all extreme points is negative, then no master problem variables exists to improve the current master problem solution.
The computational advantage of Dantzig-Wolfe decomposition arises from performing a significant amount of the computational work in the pricing problems that are roughly an order of magnitude smaller than the original problem and thus easier to solve. An aspect of the method that is of interest in the context of this paper is that the subproblems are independent of each other, and may therefore be solved concurrently.
A potential drawback of the decomposition approach is the huge size of the master problem, it has many more variables—though fewer constraints—than the original problem. In general it is not required to generate all variables explicitly but since the feasible region of the master problem is more complex than that of the original problem, the solution path may be longer. Furthermore, numerical problems may occur through the dynamic generation of variables of the master problem.
Many factors may influence the performance of a decomposition approach, so for a particular application computational experiments will be required to find out whether this solution method is suitable. Such tests may include different ways of decomposing a given problem. As a general rule for the definition of a problem decomposition, one should aim for few global constraints since it is important to be able to (re)solve the master problem quickly. In addition, the pricing problems should be constructed in such a way that they are well formed problems in their own right to avoid computational problems due to degeneracy.
The company Coco has two plants that can produce two types of cocoa powder. The first factory has a total capacity of 400 tons per month and the second of 500 tons per month. The marketing department has provided estimations for the maximum amount of every product that may be sold in each of the next four months, and also the expected sales prices. Several raw materials are used in the production with known raw material requirements per ton of finished products. Finished products and raw material may be stored at the factories from one tim period to the next, incurring a given cost per ton and per time period. The raw material storage capacity at the factories is limited to 300 tons. How should the two plants be operated during the planning period to maximize the total profit?
Let PRODS be the set of finished products, FACT the set of factories, RAW the set of raw materials, and TIMES={1,...,NT} the set of time periods under consideration.
We define decision variables makepft representing the quantity of product p made at factory f during time period t. Furthermore, to model the transition from one time period to the next and to account for the different types of cost incurred, we need several other sets of variables: sellpft, the amount of product p sold at factory f in period t; buyrft the amount of raw material r bought at f in t; and finally pstockpft and rstockrft (both defined for t=1,...,NT+1) respectively the amount of product and raw material held in stock at factory f at the beginning of period t.
Let further MXSELLpt be the maximum sales quantity of product p in period t, MXMAKEf the capacity limit of factory f, and MXRSTOCK the raw material storage capacity.
Let IPSTOCKpf be the quantity of product p initially held in stock at factory f and IRSTOCKrf the initial stock level of raw material r. We denote by CPSTOCK and CRSTOCK respectively the unit cost for storing finished product and raw material.
The objective function of maximizing the total profit is to maximize the sales revenues (REVp), minus the cost of production (CMAKEpf), buying raw material (CBUYrt), and storing finished products and raw material.
| p |
| f |
| t |
| p |
| f |
| t |
| r |
| f |
| t |
| p |
| f |
| NT+1 |
| t =2 |
| r |
| f |
| NT+1 |
| t =2 |
The possibility to store products between time periods gives rise to three sets of constraints: the inventory balance constraints for finished products (PBalpft) and for raw material (RBalrft), and the limit on the raw material storage capacity (MxRStockft). The stock pstockp,f,t+1 of product p at the beginning of t+1 is given by the stock at the beginning of t plus the production in t reduced by the amount sold on t. The stock rstockr,f,t+1 of raw material r at the beginning of t+1 is given by the corresponding stock at the beginning of t plus the amount bought in t reduced by the quantity used in production during t.
| p |
| r |
We further have two sets of capacity constraints: the production capacity of the factories is limited (constraints MxMakeft) and we can only sell up to a given maximum amount of finished products per time period (constraints MxSellft).
Below the complete mathematical model is given. The initial stock levels (t=1) of finished products and raw material are fixed to the given values.
| p |
| f |
| t |
| p |
| f |
| t |
| r |
| f |
| t |
| p |
| f |
| NT+1 |
| t =2 |
| r |
| f |
| NT+1 |
| t =2 |
| p |
| f |
| p |
| r |
We now decompose the problem described above according to production locations. Notice that this is not the only way of decomposing this problem: we may just as well choose a decomposition by products or by time periods. However, both of these choices result in a larger number of global constraints than the decomposition by factories, meaning that the master problem may become more difficult to solve.
For every factory f we obtain the following subproblem (including the sales limit constraints MxSell in the form of bounds in the submodels is not required, but may lead to better, that is, more exact or faster solutions).
| p |
| t |
| p |
| t |
| r |
| t |
| p |
| NT+1 |
| t =2 |
| r |
| NT+1 |
| t =2 |
| p |
| p |
| r |
The master problem only contains a single set of global constraints, namely the sales limit constraints MxSell (for clarity's sake, the non-negativity constraints are left out here).
| p |
| f |
| t |
| p |
| f |
| t |
| r |
| f |
| t |
| p |
| f |
| NT+1 |
| t =2 |
| r |
| f |
| NT+1 |
| t =2 |
| f |
In the decomposition algorithm, the decision variables in the master problem are expressed via the solutions (proposals) generated by the subproblems, such as
| nPROPf |
| k=1 |
where Prop_sellpftk stands for the solution value of variable sellpt in the kth proposal generated by subproblem f and Prop_costfk is the objective value this proposal. For every subproblem f we need to add a convexity constraint Convexf on the weightfk variables.
| f |
| nPROPf |
| k=1 |
| f |
| nPROPf |
| k=1 |
| nPROPf |
| k=1 |
We shall refer to this problem as the modified master problem. Without going any further into technical detail we simply remark that a correspondence exists between the solution of the original problem and those of the modified master problem.
The decomposition algorithm has several phases:
The suproblems solved in phases 1 and 2 take as their objective functions sums of the dual values from the modfied master problem. To avoid starting off with an empty master problem and hence random dual information that may be misleading we add a crash Phase 0 to our implementation that generates one proposal for each subproblem with the original objective function.
Below follows the body of the master model file. The definitions of the function bodies will be shown later in Section Master problem subroutines.
model "Coco3 Master"
uses "mmxprs","mmjobs","mmsystem"
parameters
DATAFILE = "coco2.dat"
ALG = 0 ! 0: stop phase with 1st failed subpb.
! 1: stop when all subprob.s fail
end-parameters
forward procedure process_sub_result
forward procedure solve_master(phase:integer)
forward procedure process_master_result
forward function calc_solution:real
forward procedure print_solution
declarations
PHASE_0=2 ! Event codes sent to submodels
PHASE_1=3
PHASE_2=4
PHASE_3=5
EVENT_SOLVED=6 ! Event codes sent by submodels
EVENT_FAILED=7
EVENT_READY=8
NPROD, NFACT, NRAW, NT: integer
end-declarations
initializations from DATAFILE
NPROD NFACT NRAW NT
end-initializations
declarations
PRODS = 1..NPROD ! Range of products (p)
FACT = 1..NFACT ! factories (f)
RAW = 1..NRAW ! raw materials (r)
TIME = 1..NT ! time periods (t)
nIter: integer ! Iteration counter
nPROP: array(FACT) of integer ! Counters of proposals from subprob.s
end-declarations
!**** Master problem ****
declarations
MXSELL: array(PRODS,TIME) of real ! Max. amount of p that can be sold
excessS: mpvar ! Violation of sales/buying limits
weight: array(FACT,range) of mpvar ! weights for proposals
MxSell: array(PRODS,TIME) of linctr ! Sales limit constraints
Convex: array(FACT) of linctr ! Convexity constraints
Price_convex: array(FACT) of real ! Dual price on convexity constraints
Price_sell: array(PRODS,TIME) of real ! Dual price on sales limits
end-declarations
initializations from DATAFILE
MXSELL
end-initializations
!**** Submodels ****
declarations
submod: array(FACT) of Model ! One subproblem per factory
Stopped: set of integer
modid: array(set of integer) of integer ! Model indices
end-declarations
res:= compile("g","cocoSubF.mos") ! Compile the submodel file
forall(f in FACT) do ! Load & run one submodel per product
Price_convex(f):= 1
load(submod(f), "cocoSubF.bim")
modid(getid(submod(f))):= f
run(submod(f), "Factory=" + f + ",DATAFILE=" + DATAFILE)
wait ! Wait for child model to be ready
dropnextevent
end-do
!**** Phase 0: Crash ****
nIter:=1; finished:=false
writeln("\nPHASE 0 -- Iteration ", nIter); fflush
forall(f in FACT) ! Start solving all submodels (Phase 1)
send(submod(f), PHASE_0, 0)
forall(f in FACT) do
wait ! Wait for child (termination) events
ev:= getnextevent
if getclass(ev)=EVENT_SOLVED then
process_sub_result ! Add new proposal to master problem
elif getclass(ev)=EVENT_FAILED then
finished:= true
end-if
end-do
if finished then
writeln("Problem is infeasible")
exit(1)
end-if
solve_master(1) ! Solve the updated Ph. 1 master problem
process_master_result ! Store initial pricing data for submodels
!**** Phase 1: proposal generation (feasibility) ****
repeat
noimprove:= 0
nIter+=1
writeln("\nPHASE 1 -- Iteration ", nIter); fflush
forall(f in FACT) ! Start solving all submodels (Phase 1)
send(submod(f), PHASE_1, Price_convex(f))
forall(f in FACT) do
wait ! Wait for child (termination) events
ev:= getnextevent
if getclass(ev)=EVENT_SOLVED then
process_sub_result ! Add new proposal to master problem
elif getclass(ev)=EVENT_FAILED then
noimprove += 1
end-if
end-do
if noimprove = NFACT then
writeln("Problem is infeasible")
exit(2)
end-if
if ALG=0 and noimprove > 0 then
writeln("No improvement by some subproblem(s)")
break
end-if
solve_master(1) ! Solve the updated Ph. 1 master problem
if getobjval>0.00001 then
process_master_result ! Store new pricing data for submodels
end-if
until getobjval <= 0.00001
!**** Phase 2: proposal generation (optimization) ****
writeln("\n**** PHASE 2 ****")
finished:=false
repeat
solve_master(2) ! Solve Phase 2 master problem
process_master_result ! Store new pricing data for submodels
nIter+=1
writeln("\nPHASE 2 -- Iteration ", nIter); fflush
forall(f in FACT) ! Start solving all submodels (Phase 2)
send(submod(f), PHASE_2, Price_convex(f))
forall(f in FACT) do
wait ! Wait for child (termination) events
ev:= getnextevent
if getclass(ev)=EVENT_SOLVED then
process_sub_result ! Add new proposal to master problem
elif getclass(ev)=EVENT_FAILED then
if ALG=0 then
finished:=true ! 1st submodel w/o prop. stops phase 2
else
Stopped += {modid(getfromid(ev))} ! Stop phase 2 only when no submodel
! generates a new proposal
end-if
end-if
end-do
if getsize(Stopped) = NFACT then finished:= true; end-if
until finished
solve_master(2) ! Re-solve master to integrate
! proposal(s) from last ph. 2 iteration
!**** Phase 3: solution to the original problem ****
writeln("\n**** PHASE 3 ****")
forall(f in FACT) do
send(submod(f), PHASE_3, 0) ! Stop all submodels
wait
dropnextevent
end-do
writeln("Total Profit=", calc_solution)
print_solution
end-model
The initial declarations block of this model defines a certain number of event codes that are used to identify the messages sent between this master model and its child (sub)models. The same declarations need to be repeated in the child models.
The model file cocoSubF.mos with the definition of the subproblems has the following contents.
model "Coco Subproblem (factory based decomp.)"
uses "mmxprs", "mmjobs"
parameters
Factory = 0
TOL = 0.00001
DATAFILE = "coco3.dat"
end-parameters
forward procedure process_solution
declarations
PHASE_0=2 ! Event codes sent to submodels
PHASE_1=3
PHASE_2=4
PHASE_3=5
EVENT_SOLVED=6 ! Event codes sent by submodels
EVENT_FAILED=7
EVENT_READY=8
NPROD, NFACT, NRAW, NT: integer
end-declarations
send(EVENT_READY,0) ! Model is ready (= running)
initializations from DATAFILE
NPROD NFACT NRAW NT
end-initializations
declarations
PRODS = 1..NPROD ! Range of products (p)
FACT = 1..NFACT ! factories (f)
RAW = 1..NRAW ! raw materials (r)
TIME = 1..NT ! time periods (t)
REV: array(PRODS,TIME) of real ! Unit selling price of products
CMAKE: array(PRODS,FACT) of real ! Unit cost to make product p
! at factory f
CBUY: array(RAW,TIME) of real ! Unit cost to buy raw materials
REQ: array(PRODS,RAW) of real ! Requirement by unit of product p
! for raw material r
MXSELL: array(PRODS,TIME) of real ! Max. amount of p that can be sold
MXMAKE: array(FACT) of real ! Max. amount factory f can make
! over all products
IPSTOCK: array(PRODS,FACT) of real ! Initial product stock levels
IRSTOCK: array(RAW,FACT) of real ! Initial raw material stock levels
CPSTOCK: real ! Unit cost to store any product p
CRSTOCK: real ! Unit cost to store any raw mat. r
MXRSTOCK: real ! Raw material storage capacity
make: array(PRODS,TIME) of mpvar ! Amount of products made at factory
sell: array(PRODS,TIME) of mpvar ! Amount of product sold from factory
buy: array(RAW,TIME) of mpvar ! Amount of raw material bought
pstock: array(PRODS,1..NT+1) of mpvar ! Product stock levels at start
! of period t
rstock: array(RAW,1..NT+1) of mpvar ! Raw material stock levels
! at start of period t
sol_make: array(PRODS,TIME) of real ! Amount of products made
sol_sell: array(PRODS,TIME) of real ! Amount of product sold
sol_buy: array(RAW,TIME) of real ! Amount of raw mat. bought
sol_pstock: array(PRODS,1..NT+1) of real ! Product stock levels
sol_rstock: array(RAW,1..NT+1) of real ! Raw mat. stock levels
Profit: linctr ! Profit of proposal
Price_sell: array(PRODS,TIME) of real ! Dual price on sales limits
end-declarations
initializations from DATAFILE
CMAKE REV CBUY REQ MXSELL MXMAKE
IPSTOCK IRSTOCK MXRSTOCK CPSTOCK CRSTOCK
end-initializations
! Product stock balance
forall(p in PRODS,t in TIME)
PBal(p,t):= pstock(p,t+1) = pstock(p,t) + make(p,t) - sell(p,t)
! Raw material stock balance
forall(r in RAW,t in TIME)
RBal(r,t):= rstock(r,t+1) =
rstock(r,t) + buy(r,t) - sum(p in PRODS) REQ(p,r)*make(p,t)
! Capacity limit
forall(t in TIME)
MxMake(t):= sum(p in PRODS) make(p,t) <= MXMAKE(Factory)
! Limit on the amount of prod. p to be sold
forall(p in PRODS,t in TIME) sell(p,t) <= MXSELL(p,t)
! Raw material stock limit
forall(t in 2..NT+1)
MxRStock(t):= sum(r in RAW) rstock(r,t) <= MXRSTOCK
! Initial product and raw material stock levels
forall(p in PRODS) pstock(p,1) = IPSTOCK(p,Factory)
forall(r in RAW) rstock(r,1) = IRSTOCK(r,Factory)
! Total profit
Profit:=
sum(p in PRODS,t in TIME) REV(p,t) * sell(p,t) - ! revenue
sum(p in PRODS,t in TIME) CMAKE(p,Factory) * make(p,t) - ! prod. cost
sum(r in RAW,t in TIME) CBUY(r,t) * buy(r,t) - ! raw mat.
sum(p in PRODS,t in 2..NT+1) CPSTOCK * pstock(p,t) - ! p storage
sum(r in RAW,t in 2..NT+1) CRSTOCK * rstock(r,t) ! r storage
! (Re)solve this model until it is stopped by event "PHASE_3"
repeat
wait
ev:= getnextevent
Phase:= getclass(ev)
if Phase=PHASE_3 then ! Stop the execution of this model
break
end-if
Price_convex:= getvalue(ev) ! Get new pricing data
if Phase<>PHASE_0 then
initializations from "raw:noindex"
Price_sell as "shmem:Price_sell"
end-initializations
end-if
! (Re)solve this model
if Phase=PHASE_0 then
maximize(Profit)
elif Phase=PHASE_1 then
maximize(sum(p in PRODS,t in TIME) Price_sell(p,t)*sell(p,t) + Price_convex)
else ! PHASE 2
maximize(
Profit - sum(p in PRODS,t in TIME) Price_sell(p,t)*sell(p,t) -
Price_convex)
end-if
writeln("Factory ", Factory, " - Obj: ", getobjval,
" Profit: ", getsol(Profit), " Price_sell: ",
getsol(sum(p in PRODS,t in TIME) Price_sell(p,t)*sell(p,t) ),
" Price_convex: ", Price_convex)
fflush
if getobjval > TOL then ! Solution found: send values to master
process_solution
elif getobjval <= TOL then ! Problem is infeasible (Phase 0/1) or
send(EVENT_FAILED,0) ! no improved solution found (Phase 2)
else
send(EVENT_READY,0)
end-if
until false
!-----------------------------------------------------------
! Process solution data
procedure process_solution
forall(p in PRODS,t in TIME) do
sol_make(p,t):= getsol(make(p,t))
sol_sell(p,t):= getsol(sell(p,t))
end-do
forall(r in RAW,t in TIME) sol_buy(r,t):= getsol(buy(r,t))
forall(p in PRODS,t in 1..NT+1) sol_pstock(p,t):= getsol(pstock(p,t))
forall(r in RAW,t in 1..NT+1) sol_rstock(r,t):= getsol(rstock(r,t))
Prop_cost:= getsol(Profit)
send(EVENT_SOLVED,0)
initializations to "mempipe:noindex,sol"
Factory
sol_make sol_sell sol_buy sol_pstock sol_rstock
Prop_cost
end-initializations
end-procedure
end-model
The child models are re-solved until they receive the PHASE_3 code. At every iteration they write their solution values to memory so that these can be processed by the master model.
The following three subroutines of the master model recover the solutions produced by the subproblems (process_sub_result), re-solve the master problem (solve_master), and communicate the solution of the master problem to its child models (process_master_result).
declarations
Prop_make: array(PRODS,FACT,TIME,range) of real ! Amount of products made
Prop_sell: array(PRODS,FACT,TIME,range) of real ! Amount of product sold
Prop_buy: array(RAW,FACT,TIME,range) of real ! Amount of raw mat. bought
Prop_pstock: array(PRODS,FACT,1..NT+1,range) of real ! Product stock levels
Prop_rstock: array(RAW,FACT,1..NT+1,range) of real ! Raw mat. stock levels
Prop_cost: array(FACT,range) of real ! Cost/profit of each proposal
end-declarations
procedure process_sub_result
declarations
f: integer ! Factory index
! Solution values of the proposal:
sol_make: array(PRODS,TIME) of real ! Amount of products made
sol_sell: array(PRODS,TIME) of real ! Amount of product sold
sol_buy: array(RAW,TIME) of real ! Amount of raw mat. bought
sol_pstock: array(PRODS,1..NT+1) of real ! Product stock levels
sol_rstock: array(RAW,1..NT+1) of real ! Raw mat. stock levels
pc: real ! Cost of the proposal
end-declarations
! Read proposal data from memory
initializations from "mempipe:noindex,sol"
f
sol_make sol_sell sol_buy sol_pstock sol_rstock
pc
end-initializations
! Add the new proposal to the master problem
nPROP(f)+=1
create(weight(f,nPROP(f)))
forall(p in PRODS,t in TIME) do
Prop_make(p,f,t,nPROP(f)):= sol_make(p,t)
Prop_sell(p,f,t,nPROP(f)):= sol_sell(p,t)
end-do
forall(r in RAW,t in TIME) Prop_buy(r,f,t,nPROP(f)):= sol_buy(r,t)
forall(p in PRODS,t in 1..NT+1) Prop_pstock(p,f,t,nPROP(f)):= sol_pstock(p,t)
forall(r in RAW,t in 1..NT+1) Prop_rstock(r,f,t,nPROP(f)):= sol_rstock(r,t)
Prop_cost(f,nPROP(f)):= pc
writeln("Sol. for factory ", f, ":\n make: ", sol_make, "\n sell: ",
sol_sell, "\n buy: ", sol_buy, "\n pstock: ", sol_pstock,
"\n rstock: ", sol_rstock)
end-procedure
!-----------------------------------------------------------
procedure solve_master(phase: integer)
forall(f in FACT)
Convex(f):= sum (k in 1..nPROP(f)) weight(f,k) = 1
if phase=1 then
forall(p in PRODS,t in TIME)
MxSell(p,t):=
sum(f in FACT,k in 1..nPROP(f)) Prop_sell(p,f,t,k)*weight(f,k) -
excessS <= MXSELL(p,t)
minimize(excessS)
else
forall(p in PRODS,t in TIME)
MxSell(p,t):=
sum(f in FACT,k in 1..nPROP(f)) Prop_sell(p,f,t,k)*weight(f,k) <=
MXSELL(p,t)
maximize(sum(f in FACT, k in 1..nPROP(f)) Prop_cost(f,k) * weight(f,k))
end-if
writeln("Master problem objective: ", getobjval)
write(" Weights:")
forall(f in FACT,k in 1..nPROP(f)) write(" ", getsol(weight(f,k)))
writeln
end-procedure
!-----------------------------------------------------------
procedure process_master_result
forall(p in PRODS,t in TIME) Price_sell(p,t):=getdual(MxSell(p,t))
forall(f in FACT) Price_convex(f):=getdual(Convex(f))
initializations to "raw:noindex"
Price_sell as "shmem:Price_sell"
end-initializations
end-procedure
Finally, the master model is completed by two subroutines for calculating the solution to the original problem (calc_solution), Phase 3 of the decomposition algorithm, and printing out the solution (print_solution). The solution to the original problem is obtained from the solution values of the modfied master problem and the proposals generated by the subproblems.
declarations
REV: array(PRODS,TIME) of real ! Unit selling price of products
CMAKE: array(PRODS,FACT) of real ! Unit cost to make product p
! at factory f
CBUY: array(RAW,TIME) of real ! Unit cost to buy raw materials
COPEN: array(FACT) of real ! Fixed cost of factory f being
! open for one period
CPSTOCK: real ! Unit cost to store any product p
CRSTOCK: real ! Unit cost to store any raw mat. r
Sol_make: array(PRODS,FACT,TIME) of real ! Solution value (products made)
Sol_sell: array(PRODS,FACT,TIME) of real ! Solution value (product sold)
Sol_buy: array(RAW,FACT,TIME) of real ! Solution value (raw mat. bought)
Sol_pstock: array(PRODS,FACT,1..NT+1) of real ! Sol. value (prod. stock)
Sol_rstock: array(RAW,FACT,1..NT+1) of real ! Sol. value (raw mat. stock)
end-declarations
initializations from DATAFILE
CMAKE REV CBUY CPSTOCK CRSTOCK COPEN
end-initializations
function calc_solution: real
forall(p in PRODS,f in FACT,t in TIME) do
Sol_sell(p,f,t):=
sum(k in 1..nPROP(f)) Prop_sell(p,f,t,k) * getsol(weight(f,k))
Sol_make(p,f,t):=
sum(k in 1..nPROP(f)) Prop_make(p,f,t,k) * getsol(weight(f,k))
end-do
forall(r in RAW,f in FACT,t in TIME) Sol_buy(r,f,t):=
sum(k in 1..nPROP(f)) Prop_buy(r,f,t,k) * getsol(weight(f,k))
forall(p in PRODS,f in FACT,t in 1..NT+1) Sol_pstock(p,f,t):=
sum(k in 1..nPROP(f)) Prop_pstock(p,f,t,k) * getsol(weight(f,k))
forall(r in RAW,f in FACT,t in 1..NT+1) Sol_rstock(r,f,t):=
sum(k in 1..nPROP(f)) Prop_rstock(r,f,t,k) * getsol(weight(f,k))
returned:=
sum(p in PRODS,f in FACT,t in TIME) REV(p,t) * Sol_sell(p,f,t) -
sum(p in PRODS,f in FACT,t in TIME) CMAKE(p,f) * Sol_make(p,f,t) -
sum(r in RAW,f in FACT,t in TIME) CBUY(r,t) * Sol_buy(r,f,t) -
sum(p in PRODS,f in FACT,t in 2..NT+1) CPSTOCK * Sol_pstock(p,f,t) -
sum(r in RAW,f in FACT,t in 2..NT+1) CRSTOCK * Sol_rstock(r,f,t)
end-function
!-----------------------------------------------------------
procedure print_solution
writeln("Finished products:")
forall(f in FACT) do
writeln("Factory ", f, ":")
forall(p in PRODS) do
write(" ", p, ": ")
forall(t in TIME) write(strfmt(Sol_make(p,f,t),6,1), "(",
strfmt(Sol_pstock(p,f,t+1),5,1), ")")
writeln
end-do
end-do
writeln("Raw material:")
forall(f in FACT) do
writeln("Factory ", f, ":")
forall(r in RAW) do
write(" ", r, ": ")
forall(t in TIME) write(strfmt(Sol_buy(r,f,t),6,1), "(",
strfmt(Sol_rstock(r,f,t+1),5,1), ")")
writeln
end-do
end-do
writeln("Sales:")
forall(f in FACT) do
writeln("Factory ", f, ":")
forall(p in PRODS) do
write(" ", p, ": ")
forall(t in TIME) write(strfmt(Sol_sell(p,f,t),4))
writeln
end-do
end-do
writeln("\nComputation time: ", gettime)
end-procedure
For the test cases that have been tried the solutions produced by our decomposition algorithm are close to the optimal solution, but the latter is not always reached. The reason behind this is that the decomposition algorithm is a sequence of iterations that may accumulate errors at different levels---lowering the tolerances used as stopping criterion in the submodels most of the time does not improve the solution. However, the configuration of the decomposition algorithm itself shows some impact on the solution: in phases 1 and 2 one may choose, for instance, to stop once the first submodel returns no improvement or continue until no more proposals are generated. Generating more proposals sometimes helps finding a better solution, but it also increases the number of times (sub)problems are solved and hence prolongates the solving time.
Benders decomposition is a decomposition method for solving large Mixed Integer Programming problems. Instead of solving a MIP problem that may be too large for standard solution methods all-in-one, we work with a sequence of linear and pure integer subproblems (the latter with a smaller number of constraints than the original problem). The description of the decomposition algorithm below is taken from [Hu69] where the interested reader will also find proofs of its finiteness and of the statement that it always results in the optimal solution.
Consider the following standard form of a mixed-integer programming problem (problem I).
In the above, and all through this section, we use bold letters for vectors and matrices. For instance, Cx + Dy stands for ![]()
Ci·xi +
NCTVAR
i=1
![]()
Di·yi, where NCTVAR denotes the number of continuous variables and NINTVAR the number of integer variables.
NINTVAR
i=1
For given values y' of y the problem above is reduced to a linear program (problem II)—we leave out the constant term in the objective:
The dual program of problem II is given by problem IId:
An interesting feature of the dual problem IId is that the feasible region of u is independent of y. Furthermore,
from duality theory it follows that if problem IId is infeasible or has no finite optimum solution, then the original problem
I has no finite optimum solution. Again from duality theory we know that if problem IId has a finite optimum solution u* then this solution has the same value as the optimum solution to the primal problem (that is, u*(b - By') = Cx*), and for a solution up (at a vertex p of the feasible region) we have up(b - By') ![]() Cx*. Substituting the latter into the objective of the original MIP problem we obtain a constraint of the form
Cx*. Substituting the latter into the objective of the original MIP problem we obtain a constraint of the form
To obtain the optimum solution z* of the original MIP problem (problem I) we may use the following partitioning algorithm that is known as Benders decomposition algorithm:
This algorithm is provably finite. It results in the optimum solution and at any time during its execution lower and upper bounds on the optimum solution z* can be obtained.
Our implementation of Benders decomposition will solve the following example problem with NCTVAR=3 continuous variables xi, NINTVAR=3 integer variables yi, and NC=4 inequality constraints.
| maximize | 5·x1 | + | 4·x2 | + | 3·x3 | + | 2·y1 | + | 2·y2 | + | 3·y3 | |
| x1 | - | x2 | + | 5·x3 | + | 3·y1 | + | 2·y3 | ||||
| 4·x2 | + | 3·x3 | - | y1 | + | y2 | ||||||
| 2·x1 | - | 2·x3 | + | y1 | - | y2 | + | y3 | ||||
| 3·x1 | + | 5·y1 | + | 5·y2 | + | 5·y3 | ||||||
| x, y |
||||||||||||
The master model reads in the data, defines the solution algorithm, coordinates the communication between the submodels, and prints out the solution at the end. For step 2 of the algorithm (solving the dual problem with fixed integer variables) we have the choice to solve either the primal problem and retrieve the dual solution values from the Optimizer or to define the dual problem ourselves and solve it. Model parameter ALG lets the user choose between these two options.
The main part of the master model looks as follows. Prior to the start of the solution algorithm itself all submodels are compiled, loaded, and started so that in each step of the algorithm we simply need to trigger the (re)solving of the corresponding submodel.
model "Benders (master model)"
uses "mmxprs", "mmjobs"
parameters
NCTVAR = 3
NINTVAR = 3
NC = 4
BIGM = 1000
ALG = 1 ! 1: Use Benders decomposition (dual)
! 2: Use Benders decomposition (primal)
DATAFILE = "bprob33.dat"
end-parameters
forward procedure start_solution
forward procedure solve_primal_int(ct: integer)
forward procedure solve_cont
forward function eval_solution: boolean
forward procedure print_solution
declarations
STEP_0=2 ! Event codes sent to submodels
STEP_1=3
STEP_2=4
EVENT_SOLVED=6 ! Event codes sent by submodels
EVENT_INFEAS=7
EVENT_READY=8
CtVars = 1..NCTVAR ! Continuous variables
IntVars = 1..NINTVAR ! Discrete variables
Ctrs = 1..NC ! Set of constraints (orig. problem)
A: array(Ctrs,CtVars) of integer ! Coeff.s of continuous variables
B: array(Ctrs,IntVars) of integer ! Coeff.s of discrete variables
b: array(Ctrs) of integer ! RHS values
C: array(CtVars) of integer ! Obj. coeff.s of continuous variables
D: array(IntVars) of integer ! Obj. coeff.s of discrete variables
Ctr: array(Ctrs) of linctr ! Constraints of orig. problem
CtrD: array(CtVars) of linctr ! Constraints of dual problem
MC: array(range) of linctr ! Constraints generated by alg.
sol_u: array(Ctrs) of real ! Solution of dual problem
sol_x: array(CtVars) of real ! Solution of primal prob. (cont.)
sol_y: array(IntVars) of real ! Solution of primal prob. (integers)
sol_obj: real ! Objective function value (primal)
RM: range ! Model indices
stepmod: array(RM) of Model ! Submodels
end-declarations
initializations from DATAFILE
A B b C D
end-initializations
! **** Submodels ****
initializations to "raw:noindex" ! Save data for submodels
A as "shmem:A" B as "shmem:B"
b as "shmem:b" C as "shmem:C" D as "shmem:D"
end-initializations
! Compile + load all submodels
if compile("benders_int.mos")<>0 then exit(1); end-if
create(stepmod(1)); load(stepmod(1), "benders_int.bim")
if compile("benders_dual.mos")<>0 then exit(2); end-if
if ALG=1 then
create(stepmod(2)); load(stepmod(2), "benders_dual.bim")
else
create(stepmod(0)); load(stepmod(0), "benders_dual.bim")
if compile("benders_cont.mos")<>0 then exit(3); end-if
create(stepmod(2)); load(stepmod(2), "benders_cont.bim")
run(stepmod(0), "NCTVAR=" + NCTVAR + ",NINTVAR=" + NINTVAR + ",NC=" + NC)
end-if
! Start the execution of the submodels
run(stepmod(1), "NINTVAR=" + NINTVAR + ",NC=" + NC)
run(stepmod(2), "NCTVAR=" + NCTVAR + ",NINTVAR=" + NINTVAR + ",NC=" + NC)
forall(m in RM) do
wait ! Wait for "Ready" messages
ev:= getnextevent
if getclass(ev) <> EVENT_READY then
writeln("Error occurred in a subproblem")
exit(4)
end-if
end-do
! **** Solution algorithm ****
start_solution ! 0. Initial solution for cont. var.s
ct:= 1
repeat
writeln("\n**** Iteration: ", ct)
solve_primal_int(ct) ! 1. Solve problem with fixed cont.
solve_cont ! 2. Solve problem with fixed int.
ct+=1
until eval_solution ! Test for optimality
print_solution ! 3. Retrieve and display the solution
The subroutines starting the different submodels send a `start solving' event and retrieve the solution once the submodel solving has finished. For the generation of the start solution we need to choose the right submodel, according to the settings of the parameter ALG. If this problem is found to be infeasible, then the whole problem is infeasible and we stop the execution of the model.
! Produce an initial solution for the dual problem using a dummy objective
procedure start_solution
if ALG=1 then ! Start the problem solving
send(stepmod(2), STEP_0, 0)
else
send(stepmod(0), STEP_0, 0)
end-if
wait ! Wait for the solution
ev:=getnextevent
if getclass(ev)=EVENT_INFEAS then
writeln("Problem is infeasible")
exit(6)
end-if
end-procedure
!-----------------------------------------------------------
! Solve a modified version of the primal problem, replacing continuous
! variables by the solution of the dual
procedure solve_primal_int(ct: integer)
send(stepmod(1), STEP_1, ct) ! Start the problem solving
wait ! Wait for the solution
ev:=getnextevent
sol_obj:= getvalue(ev) ! Store objective function value
initializations from "raw:noindex" ! Retrieve the solution
sol_y as "shmem:y"
end-initializations
end-procedure
!-----------------------------------------------------------
! Solve the Step 2 problem (dual or primal depending on value of ALG)
! for given solution values of y
procedure solve_cont
send(stepmod(2), STEP_2, 0) ! Start the problem solving
wait ! Wait for the solution
dropnextevent
initializations from "raw:noindex" ! Retrieve the solution
sol_u as "shmem:u"
end-initializations
end-procedure
The master model also tests whether the termination criterion is fulfilled (function eval_solution) and prints out the final solution (procedure print_solution). The latter procedure also stops all submodels:
function eval_solution: boolean
write("Test optimality: ", sol_obj - sum(i in IntVars) D(i)*sol_y(i),
" = ", sum(j in Ctrs) sol_u(j)* (b(j) -
sum(i in IntVars) B(j,i)*sol_y(i)) )
returned:= ( sol_obj - sum(i in IntVars) D(i)*sol_y(i) =
sum(j in Ctrs) sol_u(j)* (b(j) - sum(i in IntVars) B(j,i)*sol_y(i)) )
writeln(if(returned, " : true", " : false"))
end-function
!-----------------------------------------------------------
procedure print_solution
! Retrieve results
initializations from "raw:noindex"
sol_x as "shmem:x"
end-initializations
forall(m in RM) stop(stepmod(m)) ! Stop all submodels
write("\n**** Solution (Benders): ", sol_obj, "\n x: ")
forall(i in CtVars) write(sol_x(i), " ")
write(" y: ")
forall(i in IntVars) write(sol_y(i), " ")
writeln
end-procedure
In the first step of the decomposition algorithm we need to solve a pure integer problem. When the execution of this model is started it reads in the invariant data and sets up the variables. It then halts at the wait statement (first line of the repeat-until loop) until the master model sends it a (solving) event. At each invocation of solving this problem, the solution values of the previous run of the continuous problem—read from memory—are used to define a new constraint MC(k) for the integer problem. The whole model, and with it the endless loop into which the solving is embedded, will be terminated only by the `stop model' command from the master model. The complete source of this submodel (file benders_int.mos) is listed below.
model "Benders (integer problem)"
uses "mmxprs", "mmjobs"
parameters
NINTVAR = 3
NC = 4
BIGM = 1000
end-parameters
declarations
STEP_0=2 ! Event codes sent to submodels
STEP_1=3
EVENT_SOLVED=6 ! Event codes sent by submodels
EVENT_READY=8
IntVars = 1..NINTVAR ! Discrete variables
Ctrs = 1..NC ! Set of constraints (orig. problem)
B: array(Ctrs,IntVars) of integer ! Coeff.s of discrete variables
b: array(Ctrs) of integer ! RHS values
D: array(IntVars) of integer ! Obj. coeff.s of discrete variables
MC: array(range) of linctr ! Constraints generated by alg.
sol_u: array(Ctrs) of real ! Solution of dual problem
sol_y: array(IntVars) of real ! Solution of primal prob.
y: array(IntVars) of mpvar ! Discrete variables
z: mpvar ! Objective function variable
end-declarations
initializations from "raw:noindex"
B as "shmem:B" b as "shmem:b" D as "shmem:D"
end-initializations
z is_free ! Objective is a free variable
forall(i in IntVars) y(i) is_integer ! Integrality condition
forall(i in IntVars) y(i) <= BIGM ! Set (large) upper bound
send(EVENT_READY,0) ! Model is ready (= running)
repeat
wait
ev:= getnextevent
ct:= integer(getvalue(ev))
initializations from "raw:noindex"
sol_u as "shmem:u"
end-initializations
! Add a new constraint
MC(ct):= z >= sum(i in IntVars) D(i)*y(i) +
sum(j in Ctrs) sol_u(j)*(b(j) - sum(i in IntVars) B(j,i)*y(i))
minimize(z)
! Store solution values of y
forall(i in IntVars) sol_y(i):= getsol(y(i))
initializations to "raw:noindex"
sol_y as "shmem:y"
end-initializations
send(EVENT_SOLVED, getobjval)
write("Step 1: ", getobjval, "\n y: ")
forall(i in IntVars) write(sol_y(i), " ")
write("\n Slack: ")
forall(j in 1..ct) write(getslack(MC(j)), " ")
writeln
fflush
until false
end-model
Since the problems we are solving differ only by a single constraint from one iteration to the next, it may be worthwhile to save the basis of the solution to the root LP-relaxation (not the basis to the MIP solution) and reload it for the next optimization run. However, for our small test case we did not observe any improvements in terms of execution speed. For saving and re-reading the basis, the call to minimize needs to be replaced by the following sequence of statements:
declarations bas: basis end-declarations loadprob(z) loadbasis(bas) minimize(XPRS_TOP, z) savebasis(bas) minimize(XPRS_GLB, z)
The second step of our decomposition algorithm consists in solving a subproblem where all integer variables are fixed to their solution values found in the first step. The structure of the model implementing this step is quite similar to the previous submodel. When the model is run, it reads the invariant data from memory and sets up the objective function. It then halts at the line wait at the beginning of the loop to wait for a step 2 solving event sent by the master model. At every solving iteration the constraints CTR are redefined using the coefficients read from memory and the solution is written back to memory. Below follows the source of this model (file benders_cont.mos).
model "Benders (continuous problem)"
uses "mmxprs", "mmjobs"
parameters
NCTVAR = 3
NINTVAR = 3
NC = 4
BIGM = 1000
end-parameters
declarations
STEP_0=2 ! Event codes sent to submodels
STEP_2=4
STEP_3=5
EVENT_SOLVED=6 ! Event codes sent by submodels
EVENT_READY=8
CtVars = 1..NCTVAR ! Continuous variables
IntVars = 1..NINTVAR ! Discrete variables
Ctrs = 1..NC ! Set of constraints (orig. problem)
A: array(Ctrs,CtVars) of integer ! Coeff.s of continuous variables
B: array(Ctrs,IntVars) of integer ! Coeff.s of discrete variables
b: array(Ctrs) of integer ! RHS values
C: array(CtVars) of integer ! Obj. coeff.s of continuous variables
Ctr: array(Ctrs) of linctr ! Constraints of orig. problem
sol_u: array(Ctrs) of real ! Solution of dual problem
sol_x: array(CtVars) of real ! Solution of primal prob. (cont.)
sol_y: array(IntVars) of real ! Solution of primal prob. (integers)
x: array(CtVars) of mpvar ! Continuous variables
end-declarations
initializations from "raw:noindex"
A as "shmem:A" B as "shmem:B"
b as "shmem:b" C as "shmem:C"
end-initializations
Obj:= sum(i in CtVars) C(i)*x(i)
send(EVENT_READY,0) ! Model is ready (= running)
! (Re)solve this model until it is stopped by event "STEP_3"
repeat
wait
dropnextevent
initializations from "raw:noindex"
sol_y as "shmem:y"
end-initializations
forall(j in Ctrs)
Ctr(j):= sum(i in CtVars) A(j,i)*x(i) +
sum(i in IntVars) B(j,i)*sol_y(i) >= b(j)
minimize(Obj) ! Solve the problem
! Store values of u and x
forall(j in Ctrs) sol_u(j):= getdual(Ctr(j))
forall(i in CtVars) sol_x(i):= getsol(x(i))
initializations to "raw:noindex"
sol_u as "shmem:u" sol_x as "shmem:x"
end-initializations
send(EVENT_SOLVED, getobjval)
write("Step 2: ", getobjval, "\n u: ")
forall(j in Ctrs) write(sol_u(j), " ")
write("\n x: ")
forall(i in CtVars) write(getsol(x(i)), " ")
writeln
fflush
until false
end-model
To start the decomposition algorithm we need to generate an initial set of values for the continuous variables. This can be done by solving the dual problem in the continuous variables with a dummy objective function. A second use of the dual problem is for Step 2 of the algorithm, replacing the primal model we have seen in the previous section. The implementation of this submodel takes into account these two cases: within the solving loop we test for the type (class) of event that has been sent by the master problem and choose the problem to be solved accordingly.
The main part of this model is implemented by the following Mosel code (file benders_dual.mos).
model "Benders (dual problem)"
uses "mmxprs", "mmjobs"
parameters
NCTVAR = 3
NINTVAR = 3
NC = 4
BIGM = 1000
end-parameters
forward procedure save_solution
declarations
STEP_0=2 ! Event codes sent to submodels
STEP_2=4
EVENT_SOLVED=6 ! Event codes sent by submodels
EVENT_INFEAS=7
EVENT_READY=8
CtVars = 1..NCTVAR ! Continuous variables
IntVars = 1..NINTVAR ! Discrete variables
Ctrs = 1..NC ! Set of constraints (orig. problem)
A: array(Ctrs,CtVars) of integer ! Coeff.s of continuous variables
B: array(Ctrs,IntVars) of integer ! Coeff.s of discrete variables
b: array(Ctrs) of integer ! RHS values
C: array(CtVars) of integer ! Obj. coeff.s of continuous variables
sol_u: array(Ctrs) of real ! Solution of dual problem
sol_x: array(CtVars) of real ! Solution of primal prob. (cont.)
sol_y: array(IntVars) of real ! Solution of primal prob. (integers)
u: array(Ctrs) of mpvar ! Dual variables
end-declarations
initializations from "raw:noindex"
A as "shmem:A" B as "shmem:B"
b as "shmem:b" C as "shmem:C"
end-initializations
forall(i in CtVars) CtrD(i):= sum(j in Ctrs) u(j)*A(j,i) <= C(i)
send(EVENT_READY,0) ! Model is ready (= running)
! (Re)solve this model until it is stopped by event "STEP_3"
repeat
wait
ev:= getnextevent
Alg:= getclass(ev)
if Alg=STEP_0 then ! Produce an initial solution for the
! dual problem using a dummy objective
maximize(sum(j in Ctrs) u(j))
if(getprobstat = XPRS_INF) then
writeln("Problem is infeasible")
send(EVENT_INFEAS,0) ! Problem is infeasible
else
write("**** Start solution: ")
save_solution
end-if
else ! STEP 2: Solve the dual problem for
! given solution values of y
initializations from "raw:noindex"
sol_y as "shmem:y"
end-initializations
Obj:= sum(j in Ctrs) u(j)* (b(j) - sum(i in IntVars) B(j,i)*sol_y(i))
maximize(XPRS_PRI, Obj)
if(getprobstat=XPRS_UNB) then
BigM:= sum(j in Ctrs) u(j) <= BIGM
maximize(XPRS_PRI, Obj)
end-if
write("Step 2: ")
save_solution ! Write solution to memory
BigM:= 0 ! Reset the 'BigM' constraint
end-if
until false
This model is completed by the definition of the subroutine save_solution that writes the solution to memory and informs the master model of it being available by sending the EVENT_SOLVED message.
! Process solution data
procedure save_solution
! Store values of u and x
forall(j in Ctrs) sol_u(j):= getsol(u(j))
forall(i in CtVars) sol_x(i):= getdual(CtrD(i))
initializations to "raw:noindex"
sol_u as "shmem:u" sol_x as "shmem:x"
end-initializations
send(EVENT_SOLVED, getobjval)
write(getobjval, "\n u: ")
forall(j in Ctrs) write(sol_u(j), " ")
write("\n x: ")
forall(i in CtVars) write(getdual(CtrD(i)), " ")
writeln
fflush
end-procedure
end-model
The optimal solution to our small test problem has the objective function value 18.1852. Our program produces the following output, showing that the problem is solved to optimality with 3 iterations (looping around steps 1 and 2) of the decomposition algorithm:
**** Start solution: 4.05556 u: 0.740741 1.18519 2.12963 0 x: 0.611111 0.166667 0.111111 **** Iteration: 1 Step 1: -1146.15 y: 1000 0 0 Slack: 0 Step 2: 1007 u: 0 1 0 0 x: 0 251.75 0 Test optimality: -3146.15 = 1007 : false **** Iteration: 2 Step 1: 17.0185 y: 3 0 0 Slack: 0 -1.01852 Step 2: 12.5 u: 0 1 2.5 0 x: 0.5 2.5 0 Test optimality: 11.0185 = 12.5 : false **** Iteration: 3 Step 1: 18.1852 y: 2 0 0 Slack: 0 -5.18519 -0.185185 Step 2: 14.1852 u: 0.740741 1.18519 2.12963 0 x: 1.03704 2.22222 0.037037 Test optimality: 14.1852 = 14.1852 : true **** Solution (Benders): 18.1852 x: 1.03704 2.22222 0.037037 y: 2 0 0
The examples in this white paper show how to use the functionality provided by the mmjobs module. Without giving an exhaustive overview of the technical possibilities they provide starting points for implementation of, and experimentation with, parallel solving and other multi-problem solution approaches.
Any solver module available for Mosel may be used in conjunction with mmjobs. However, parallel solving of multiple problems with the same solver is only possible if the underlying solver can work in a multi-threaded environment. This is the case for Xpress-Optimizer and its derivates (QP, SLP, SP) as well as for Xpress-Kalis.