Edge-Flipping Distance Between Triangulations - Benchmark Instances, by Y. C. Soares, P. J. de Rezende and C. C. de Souza

Citing this page:

    Use the BibTeX entry:

    @Misc{efdtp-instances-page,
     author = {Y. C. Soares, P. J. de Rezende and C. C. de Souza},
     title = {Edge-Flipping Distance Between Triangulations -- Benchmark Instances},
     year = {2016},
     note = {{\sl www.ic.unicamp.br/$\sim$cid/Problem-instances/Triangulation-Flip-Distance}}
    }

Abstract

In our original paper, we proposed practical heuristics for the problem of computing the Edge-Flipping Distance Between Triangulations (EFDTP). In [3], Hanke et al. established an upper bound for the problem, along with a high-level algorithm that computes a solution with that bound. We extended that algorithm with a randomized greedy approach, proposed a new greedy strategy and implemented them in order to compare their performance. Extensive computational tests carried out on 240 instances of various sizes and classes revealed that the original algorithm was effective at obtaining good solutions for smaller instances. However, the randomized heuristic in conjunction with the novel greedy strategy lead to improved solution quality for larger cases. Our contribution includes the first experimental analysis of six increasingly efficacious methods for solving the EFDTP.


Problem Description

Given any two triangulations of one point-set, we can define the flip distance between them as the smallest number of edge flips required to transform one into the other. This naturally leads to the optimization problem of determining the flip distance between any two triangulations of a point set. In 2012, this problem was shown to be NP-complete by Lubiw and Pathak [5], and to be APX-hard by Pilz [6].


Instance Set

To test the algorithms, we generated instances with the number of points N ∈ {100, 150, 200, 250}. For each value of N and each of the two instance classes (random and star), 5 different points sets were created and, for each of them, 6 different pairs of triangulations we produced, resulting in a total of 240 distinct instances in our benchmark.
The directories are named according to the description above.
All the instances' point sets were generated with only 3 points in the convex hull.
The instance packages and generated figures can be downloaded here:

Instance Format

Input
The proposed instance input format is explained below with an example.
After the token 'N': the number of points N in a single line.
After the token 'P': N lines with the x and y coordinates of each point. One point per line.
After the token 'S': the source triangulation, with each edge linking two points as ordered by the previous chunk 0-indexed. A line with '0 0' denotes the end of a triangulation
After the token 'D': the destination triangulation, in the same format as the source triangulation.
Output
The output format is also illustrated with an example. After the token 'V': the solution value, i.e. the number of flips in the sequence. (Should be minimized)
After the token 'F': the flip sequence. A list of edges to be flipped in sequential order.
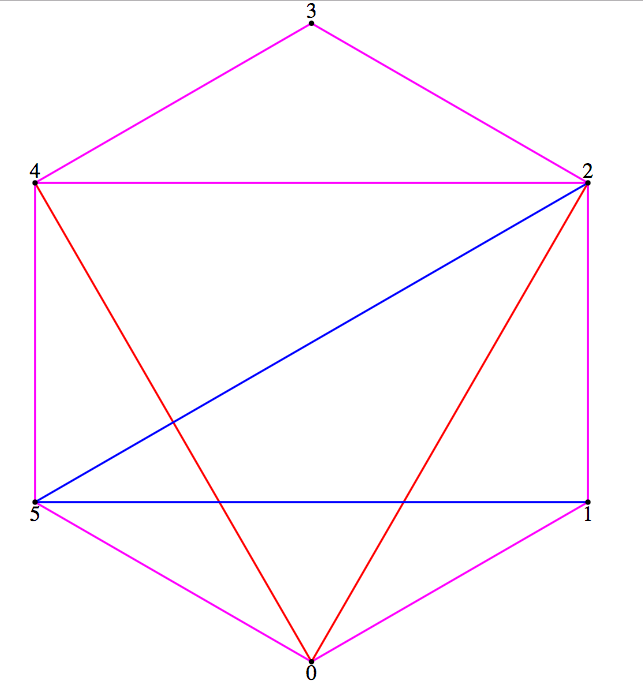
Please refer to the simple example instance and the respective figure and output:
  • Simple instance text input file
  • Simple instance svg image
  • Simple instance output file
      • In this illustration, red edges denote edges in the source triangulation, blue ones denote edges in the destination triangulation and magenta ones denote common edges. Note that edges in the convex hull are present in any triangulation.


      References

      • [1] O. Aichholzer, W. Mulzer, and A. Pilz. Flip distance between triangulations of a simple polygon is NP-complete. Discrete & Computational Geometry, 54(2):368–389, 2015.
      • [2] J. Demšar. Statistical comparisons of classifiers over multiple data sets. The Journal of Machine Learning Research, 7:1–30, Dec. 2006.
      • [3] S. Hanke, T. Ottmann, and S. Schuierer. The edge-flipping distance of triangulations. Journal of Universal Computer Science, 2(8):570–579, 1996.
      • [4] C. L. Lawson. Transforming triangulations. Discrete Mathematics, 3(4):365 – 372, 1972.
      • [5] A. Lubiw and V. Pathak. Flip distance between two triangulations of a point set is NP-complete. Computational Geometry, 49:17–23, 2015.
      • [6] A. Pilz. Flip distance between triangulations of a planar point set is APX-hard. Computational Geometry Theory and Applications, 47(5):589–604, July 2014.
      • [7] D. D. Sleator, R. E. Tarjan, and W. P. Thurston. Rotation distance, triangulations, and hyperbolic geometry. Journal of the American Mathematical Society, 1:647–681, 1988.


      Contacts

      • Pedro J. de Rezende:     homepage    
      • Cid C. de Souza:     homepage    
      • Yuri C. P. Soares::     homepage


      Research supported by: