The Perfect Awareness Problem - Benchmark Instances by F. de C. Pereira, P. J. de Rezende and C. C. de Souza

Citing this page

Use the BibTeX entry:

@Misc{pap-instances-page,
 author = {Felipe de C. Pereira and Pedro J. de Rezende and Cid C. de Souza},
 title = {The Perfect Awareness Problem - Benchmark Instances},
 year = {2020},
 note = {{\sl www.ic.unicamp.br/\textasciitilde cid/Problem-instances/Perfect-Awareness-Problem}}
}

Problem description

The Perfect Awareness Problem (PAP) is \({\sf NP}\)-hard and was first proposed in 2019 by Cordasco et. al. [1]. The PAP models the spreading of information on social networks. In this problem, we seek to find a smallest subset of seminal individuals that are sufficient to ascertain that a given news reaches everyone on a network, under certain dissemination restrictions. We can model the dissemination process by representing the network as an unweighted undirected graph \(G = (V,E)\), where each vertex represents an individual and an edge \(\{u,v\}\) is in \(E\) whenever \(u,v \in V\) can communicate (we identify each vertex with the individual that it represents). We denote the neighborhood of \(u\in V\) by \(N(u)=\{v\in V \;|\; \{u,v\}\in E\}\), the degree of \(u\) by \(d(u)\), and regard that the passage of time is discretized in rounds. In each round \(\tau \in \mathbb{N}\), every vertex is either ignorant, aware or spreader regarding the information being disseminated. We denote by \(S_\tau \subseteq V\) and \(A_\tau \subseteq V\) the sets of vertices that are spreaders and aware at round \(\tau\), respectively. Initially, at \(\tau = 0\), all vertices are ignorant, except for those in \(S_0\), which is called the seed set, and the vertices in \(S_0\) are the seeds. Given a threshold function \(t: V \rightarrow \mathbb{N}^+\), the spreading procedure occurs under the following rules. For all \(\tau \geq 1\), a vertex \(v\) is aware at round \(\tau\), that is, \(v \in A_\tau\), iff \(v \in S_0\) or \(|N(v) \cap S_{\tau-1}| \geq 1\). Also, \(v \in S_\tau\) iff \(v \in S_0\) or \(|N(v) \cap S_{\tau-1}| \geq t(v)\). This propagation process stops when \(S_{\rho-1} = S_{\rho}\) for some \(\rho > 1\). If \(A_\rho = V\), then all vertices are aware at the end of the propagation. In this case, the seed set \(S_0\) is called a perfect seed set. So, given an instance of PAP, the objective is to find a perfect seed set of minimum size. The pictures below show an example of the process of spreading in one instance of the PAP, where the thresholds associated with each vertex are indicated inside the circles. For each round, the spreaders are represented in green, the aware vertices in yellow and the ignorant ones in white. For that example, the seed set is formed by vertices \(a\) and \(b\), and it consists in a optimal solution.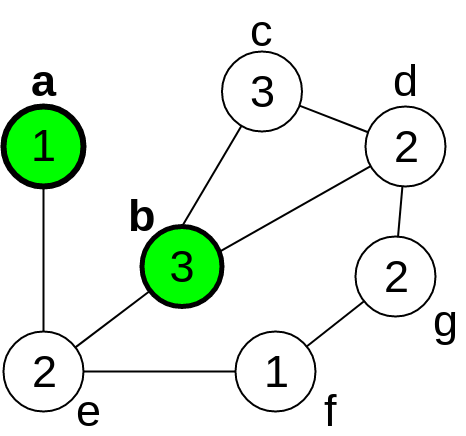

(a) \(\tau = 0\)

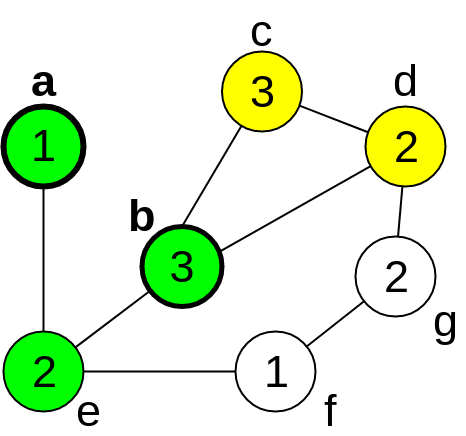
(b) \(\tau = 1\)

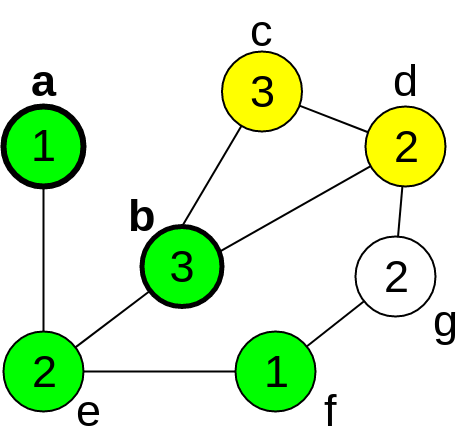
(c) \(\tau = 2\)

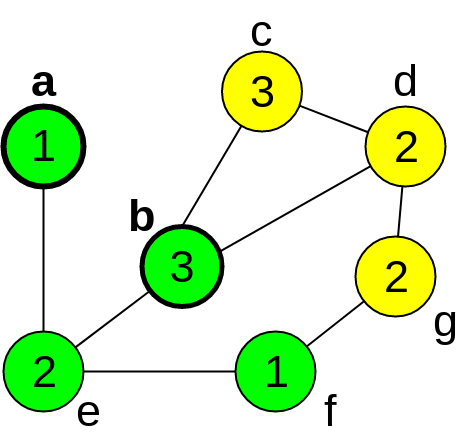
(d) \(\tau = 3\)

Social Network Generator

The literature shows that most real networks exhibit two main characteristics: growth and preferential attachment of new individuals. A widely used algorithm for generating graphs with these attributes is called the Barábasi-Albert method (BA) [2], and it works as follows. Suppose we wish to produce a connected graph \(G = (V, E)\) with \(n\) vertices. Then, we pick an integer \(k < n\) and start off \(G\) with \(|V| = k\) and \(E = \emptyset\). Next, a new vertex is added and connected to the first \(k\) vertices. Iteratively, for a total of \(n-k-1\) times, a new vertex, say \(v\), is added and \(k\) previously inserted vertices are chosen to be connected to \(v\). The probability of selecting a vertex \(u \neq v\) to be one of \(v\)'s neighbors is given by \(P(u) = d(u)/\sum_{w \in V-\{v\}} d(w)\). In the end, \(G\) will have \(|V| = n\) vertices and \(|E| = (n-k)k = nk - k^2\) edges. Notice that once \(n\) is established, the final number of edges depends solely on the choice of \(k\). Denote by \(|E|_{\min}\) and \(|E|_{\max}\) the minimum and maximum number of edges that can thus be generated, respectively. Since \(1 \leq k \leq n-1\), \(|E|_{\min} = n-1\) and \(|E|_{\max} = \lfloor n^2/4 \rfloor\). We now describe how a simple modification allows BA to generate graphs of \(n\) vertices with exactly \(m\) edges, for any \(m\), \(|E|_{\min} \leq m \leq |E|_{\max}\). To this end, we pick \(k\) as \(\lfloor x \rfloor\) where \(x\) is the smallest of the roots of \(x^2 - nx + m = 0\). Then, we proceed with the standard BA described earlier, obtaining a graph with \(|V| = n\) vertices and \(|E| = nk - k^2\) edges. If \(|E| = m\), as desired, we are done. However, if \(|E| < m\), we add \(m - |E|\) new edges as follows. Firstly, we randomly choose a vertex \(v\) to be an endpoint of a new edge. Next, we choose the other endpoint \(u \neq v\) according to the probability \(P(u)\). This process is repeated up until we get \(|E| = m\). This modification allows for complete control over the final number of edges, preserving the graph property for preferential adjacency, and adds no more than \(2k\) extra edges. This modification of the BA algorithm is called BA-RSP. The following compressed file contains an implementation of the BA-RSP graph generator in Python 3.

BA_RSP_Graph_Generator.tat.gz (13.6kB)

The input for BA-RSP is composed by a single line

     <\(n\)> <\(m \)> <seed>

where

  • \(n\): Number of vertices of the generated graph.
  • \(m\): Number of edges of the generated graph..
  • seed (optional): Seed used for the pseudorandom number generator (for the sake of reproducibility).

PAP Instance Files

We used BA-RSP to generate 840 graphs that can be used to compose PAP instances. The threshold function is usually defined as a fraction of the degree of each vertex [1] and is not included in the input file.
  • \(n\): Number of vertices of the generated graph.
  • \(m\): Number of edges of the generated graph.
  • \(k\): Parameter used in the BA algorithm that corresponds to \(\lfloor x \rfloor\), where \(x\) is the smallest of the roots of \(x^2 - nx + m = 0\).
  • \(i\): The \(i\)-th graph generated using the same values for \(n\) and \(m\).
  • seed: Seed used for generating the graph.
Each file is named according to the following pattern:

     <\(n\)>_<\(m\)>_<\(k\)>_social_<\(i\)>.in

All these files are in the following format. The first 4 lines correspond to:

     <seed>
     <\(k\)>
     <\(n\)>
     <\(m\)>

Each one of the \(m\) remaining lines contains:

     <\(u\;v\)>

where \(u,v \in \{0, 1, 2, \dots, n - 1\}\) are the endpoints of the edge \(\{u,v\}\) of the graph. Therefore, we only generate graphs where each vertex has at least one edge incident to it and its id appears in all of its edges.

The following compressed file contains the data files of all 840 graphs.

PAP_Instance_Graphs.tar.gz (32.8MB)

Furthermore, for each graph generated as described above, we complete building an instance \(\{G, t\}\) of PAP by setting \(t(v) = \lceil 0.5 \cdot d(v) \rceil\), which is called is the "majority threshold function" in [1]. In this way, we end up with a total of \(840\) instances.

PAP Solution Files

We solved those instances using our own heuristic for PAP based on the meta-heuristic Greedy Randomized Adaptive Search Procedure [3]. Each solution file has the same name as the input file, except for the extension ".sol". All these files are in the following format. The first line has an integer \(z\) indicating the value of the solution, that is, the size of the perfect seed set. Each one of the remaining \(z\) lines contains an integer that corresponds to the id of a vertex belonging to the perfect seed set.

The following compressed file contains the solution files of all 840 instances.

PAP_Solutions.tar.gz (27.2kB)

Acknowledgments

This work was supported in part by the Brazilian National Council for Scientific and Technological Development (CNPq), Grants #313329/2020-6, #130838/2019-5, #309627/2017-6; São Paulo Research Foundation(FAPESP), Grants #2020/09691-0, #2019/22297-1, #2018/26434-0, #2014/12236-1; Fund for Support to Teaching, Research and Outreach Activities (FAEPEX).

References

Address

Felipe de C. Pereira, Pedro J. de Rezende and Cid C. de Souza
University of Campinas
Institute of Computing
Avenida Albert Einstein, 1251
13083-852 Campinas, SP, Brazil
Phone: +55 19 3521.5877
e-mail: